
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.| 队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | m | 3.41 | 90% | n |
| 八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
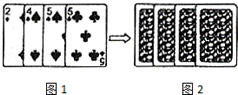 四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 10 | 15 | 20 | 25 | 20 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | 丙 | 丁 | |
| ∠C(单位:度) | 34 | 36 | 38 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com