
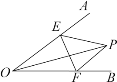
【题目】如图,∠AOB = 30°,点P是∠AOB内任意一点,且OP = 7,点E和点F分别是射线OA和射线OB上的动点,则△PEF周长的最小值是______.
【答案】7
【解析】
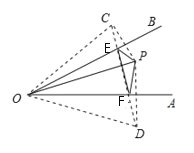
设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长最小.
分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点E、F,连接OP、OC、OD、PE、PF.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PE=CE,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PF=DF,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=7,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=7.
∴△PEF的周长的最小值=PE+EF+PF=CE+EF+DF≥CD=7.
故答案为7.


科目:初中数学 来源: 题型:
【题目】(问题探究)小敏在学习了Rt△ABC的性质定理后,继续进行研究.
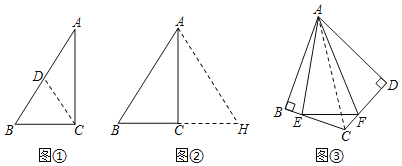
(1)(i)她发现图①中,如果∠A=30°,BC与AB存在特殊的数量关系是 ;
(ii)她将△ABC沿AC所在的直线翻折得△AHC,如图②,此时她证明了BC和AB的关系;请根据小敏证明的思路,补全探究的证明过程;
猜想:如果∠A=30°,BC与AB存在特殊的数量关系是 ;
证明:△ABC沿AC所在的直线翻折得△AHC,
(2)如图③,点E、F分别在四边形ABCD的边BC、CD上,且∠B=∠D=90°,连接AE、AF、EF,将△ABE、△ADF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形,连接AC,若∠EAF=30°,AB2=27,则△CEF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )
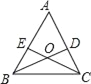
A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
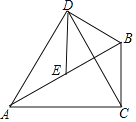
(1)求证:△ADE≌△CDB;
(2)若BC=1,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:利用多项式的乘法法则,可以得到![]() ,反过来,则有
,反过来,则有![]() 利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子
利用这个式子可以将某些二次项系数是1的二次三项式分解因式。例如:将式子![]() 分解因式.这个式子的常数项
分解因式.这个式子的常数项![]() ,一次项系数
,一次项系数![]() ,所以
,所以![]() .
.
解:![]() .
.
上述分解因式![]() 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).
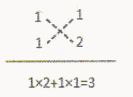
请仿照上面的方法,解答下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() ;
;
(3)若![]() 可分解为两个一次因式的积,写出整数P的所有可能值.
可分解为两个一次因式的积,写出整数P的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某村要设计修建一条引水渠,渠道的横断面为等腰梯形,渠道底面宽0.8m,渠道内坡度是1:0.5.引水时,水面要低于渠道上沿0.2m,水流的横断面(梯形ABFE)的面积为1.3m2,求水渠的深度h.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向内旋转35°到达ON位置,此时点A,C的对应位置分别是点B,D,测量出∠ODB=25°,点D到点O的距离为30cm,求滑动支架BD的长.
(结果精确到1cm,参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.
(1)请说出这个几何体模型的最确切的名称是__ __;
(2)如图②是根据 a,h的取值画出的几何体的主视图和俯视图(图中的粗实线表示的正方形(中间一条虚线)和三角形),请在网格中画出该几何体的左视图;
(3)在(2)的条件下,已知h=20 cm,求该几何体的表面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com