
 如图,已知等边△ABC,P为AC延长线上一点,以PA为边作等边△APE,EC延长线交BP于M,连接AM,求证:
如图,已知等边△ABC,P为AC延长线上一点,以PA为边作等边△APE,EC延长线交BP于M,连接AM,求证:分析 (1)根据等边三角形的性质推出AE=AP,AC=AB,∠EAC=∠PAB=60°,证出△EAC≌△PAB即可;
(2)求出∠PME=∠EAC=60°,推出A、M、P、E四点共圆,根推出∠EMP=∠EAP=60°即可.
解答 证明:(1)∵△ABC,△APE是等边三角形,
∴AE=AP,AC=AB,∠EAC=∠PAB=60°,
在△EAC与△PAB中,
∵$\left\{\begin{array}{l}{AE=AP}\\{∠EAC=∠PAB}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△PAB(SAS),
∴BP=CE;
(2)∵△EAC≌△PAB,
∴∠AEC=∠APB,
∵∠ECA=∠PCM,∠AEC+∠EAC+∠ECA=180°,∠APB+∠PCM+∠PMC=180°,
∴∠PME=∠EAC=60°,
∴A、M、P、E四点共圆,
∴∠EMP=∠EAP=60°.
点评 本题考查等边三角形的性质,全等三角形的性质和判定,圆内接四边形的性质的应用,主要考查学生的推理能力.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明在拼图时,发现8个大小一样的小长方形,如图(1)所示,恰好可以拼成一个大的长方形.小红看见了,说“我来试一试”,结果小红七拼八凑,拼成如图(2)那样的正方形,中间恰好是2mm的小正方形.求图(2)大正方形的面积.
小明在拼图时,发现8个大小一样的小长方形,如图(1)所示,恰好可以拼成一个大的长方形.小红看见了,说“我来试一试”,结果小红七拼八凑,拼成如图(2)那样的正方形,中间恰好是2mm的小正方形.求图(2)大正方形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
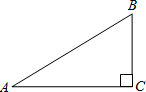 如图,在Rt△ABC中,∠ACB=90°,用尺规在BC边上找一点O,使得以点O为圆心,OC为半径的圆与AB相切,并画出⊙O(保留作图痕迹,不写作法)
如图,在Rt△ABC中,∠ACB=90°,用尺规在BC边上找一点O,使得以点O为圆心,OC为半径的圆与AB相切,并画出⊙O(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 处理污水量(吨/月) | 240 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com