
 +k)k,k为实数.
+k)k,k为实数. 是否为一定值?若是,请求出该定值;若不是,请说明理由;
是否为一定值?若是,请求出该定值;若不是,请说明理由; =k,
=k, =
=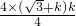 =
= k,
k, k),对称轴方程x=k.
k),对称轴方程x=k. );
); );
); ).
). x,画出图象.
x,画出图象.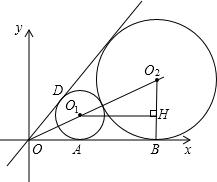
 x上取一点(1,
x上取一点(1, )可得tan∠DOA=
)可得tan∠DOA=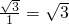 ,
, =
=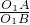 =
= ,
,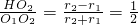 ,
, =
= ,即为定值.
,即为定值. b,0),
b,0),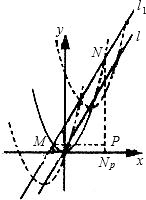
 x+b,
x+b, ,
, x-b=0,
x-b=0, ,x1x2=-b,
,x1x2=-b,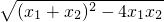 =
=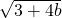 =|MP|,
=|MP|, ,
, ,
, x+
x+ .
. k),可得出无论k取什么值,横坐标和纵坐标的比例关系是不变的,因此抛物线的顶点在正比例函数的图象上,且斜率为
k),可得出无论k取什么值,横坐标和纵坐标的比例关系是不变的,因此抛物线的顶点在正比例函数的图象上,且斜率为 .
.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点;
个单位后其顶点恰好在y轴上,求抛物线C的解析式及其上的不动点;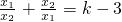 成立?若存在,求出k的值;若不存在,请说明理由.
成立?若存在,求出k的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 +k)k,k为实数.
+k)k,k为实数. 是否为一定值?若是,请求出该定值;若不是,请说明理由;
是否为一定值?若是,请求出该定值;若不是,请说明理由;查看答案和解析>>
科目:初中数学 来源:2003年湖南省长沙市中考数学试卷(解析版) 题型:解答题
 +k)k,k为实数.
+k)k,k为实数. 是否为一定值?若是,请求出该定值;若不是,请说明理由;
是否为一定值?若是,请求出该定值;若不是,请说明理由;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com