
分析 根据三角形两边长为8和6,可以得到第三边的取值范围,由第三边长是一元二次方程x2-8x+12=0的根,从而可以得到第三边的长,进而得到该三角形的周长和面积.
解答 解:∵x2-8x+12=0
∴(x-2)(x-6)=0,
得x=2或x=6,
∵三角形两边长为8和6,
∴2<第三边<14,
∵第三边长是一元二次方程x2-8x+12=0的根,
∴第三边的长是6,
∴该三角形的周长是:8+6+6=20,
面积是:$\frac{8×\sqrt{{6}^{2}-{4}^{2}}}{2}$=8$\sqrt{5}$,
故答案为:20和8$\sqrt{5}$.
点评 本题考查解一元二次方程--因式分解法、三角形的面积、三角形三边的关系,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:选择题
| A. | 2,-3,4 | B. | 2,-4,-3 | C. | 2,4,-3 | D. | 2,-3,-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内含 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
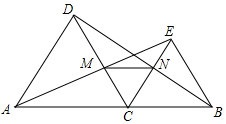 如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com