Question

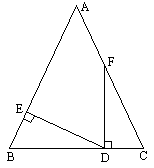
如图所示，△ABC中，∠B＝∠C，点F在AC上，过F作FD⊥BC于D，过D作DE⊥AB于E．若∠AFD＝，试求∠EDF的度数．

Answer 1

答案：
解析：

拓展延伸： 　　本题涉及知识点较多，解法较灵活，解此类题的关键是准确把握定义、定理，借助题设条件，结合图形，从中挖掘解题思路，得到正确结论． 　　答案：解法1：∵∠AFD＝，∴∠DFC＝－∠AFD＝(邻补角定义)． 　　又∵FD⊥BC于D，∴∠FDC＝(垂直定义)． 　　∴∠DFC＋∠C＝(直角三角形中两锐角互余)． 　　∴∠C＝－∠DFC＝－＝．∴∠B＝． 　　又∵DE⊥AB于E，∴∠DEB＝，又∠B＝． 　　∴∠BDE＝． 　　∴∠EDF＝－∠BDE－∠FDC＝－－＝． 　　解法2：同解法1可求出∠FDC＝∠BED－，∠C＝， 　　又∵∠BDE＋∠EDF＋∠FDC＝(平角定义)， 　　∴∠BDE＋∠EDF＝． 　　又因为∠B＋∠BDE＝，∴∠EDF＝∠B(同角的余角相等)． 　　∴∠EDF＝∠B＝∠C＝． 　　剖析：由∠AFD＝1及平角定义得到∠CFD的度数后，利用直角三角形中两锐角互余等知识可求出∠EDF度数．