
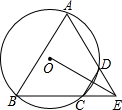
 如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.分析 (1)根据圆内接四边形的性质得到∠A=∠DCE,根据等腰三角形的性质得到∠DCE=∠DEC,等量代换证明结论;
(2)根据垂径定理得到OE是CD的垂直平分线,根据题意证明△DEC为等边三角形,证明结论.
解答 证明:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠A=∠DCE,
∵DC=DE,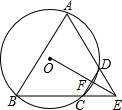
∴∠DCE=∠DEC,
∴∠A=∠AEB;
(2)∵DC⊥OE,
∴DF=CF,
∴OE是CD的垂直平分线,
∴ED=EC,又DE=DC,
∴△DEC为等边三角形,
∴∠AEB=60°,又∠A=∠AEB,
∴△ABE是等边三角形.
点评 本题考查的是圆内接四边形的性质和垂径定理的应用,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键.


科目:初中数学 来源: 题型:选择题
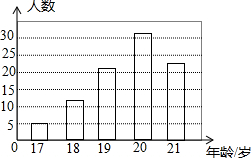 在6月26日“国际禁毒日”来临之际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
在6月26日“国际禁毒日”来临之际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com