
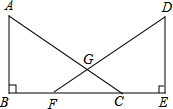
 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.求证:
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE.求证:分析 (1)由条件先得出BC=EF和∠B=∠E,再根据边角边就可以判断△ABC≌△DEF,利用全等三角形的性质即可证明:AC=DF;
(2)利用△ABC≌△DEF,得出∠ACB=∠DFE,利用等角对等边可证出GF=GC,最后得出AG=DG.
解答 证明:(1)∵BF=CE,
∴BF+CF=CE+CF,
即BC=EF.
∵AB⊥BE,DE⊥BE,
∴∠B=∠E=90°.
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{∠B=∠E}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴AC=DF,
(2)∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴GF=CG,
∴AG=DG.
点评 本题考查了全等三角形的判定及性质的运用,垂直的定义,掌握三角形全等的判定方法是解决问题的关键.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:选择题
 如图,甲乙两人沿着周长为1200米的正方形围墙外围进行猫抓老鼠的游戏,他们分别从两个对角逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过多长时间甲就能看到乙?( )
如图,甲乙两人沿着周长为1200米的正方形围墙外围进行猫抓老鼠的游戏,他们分别从两个对角逆时针同时出发,如果甲每分钟走90米,乙每分钟走70米,那么经过多长时间甲就能看到乙?( )| A. | 16分40秒 | B. | 30分 | C. | 15分 | D. | 14分40秒 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
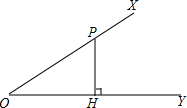 如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )
如图,P为∠XOY上一点,作PH⊥OY于H,对于sin2∠XOY+cos2∠XOY的大小,下列说法正确的是( )| A. | 与点P的位置有关 | B. | 与PH的长度有关 | ||
| C. | 与∠XOY的大小有关 | D. | 与点P的位置和∠XOY的大小都无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com