
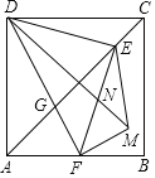
【题目】如图,正方形ABCD中,AD=6,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若AF=2,则![]() 的面积为__.
的面积为__.
【答案】![]()
【解析】
如图,取DF的中点K,连接AK,EK.连接GM交EF于H.首先证明△DEF是等腰直角三角形求出DE,EF,解直角三角形求出EN,MH即可解决问题.
解:如图,取DF的中点K,连接AK,EK.连接GM交EF于H.
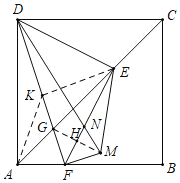
∵四边形ACD是正方形,
∴AD=AB=6,∠DAB=90°,AB∥CD,∠DAC=∠CAB=45°,
∵DE⊥EF,
∴∠DEF=∠DAF=90°,
∵DK=KF,
∴KA=KD=KF=KE,
∴A,F,E,D四点共圆,
∴∠DFE=∠DAE=45°,
∴∠EDF=∠EFD=45°,
∴DE=EF,
∵AF=2,AD=6,
∴DF=![]() ,
,
∴DE=EF=![]() ,
,
∵AF∥CD,
∴![]() ,
,
∴FG=FM=![]() ,
,
∴GM=![]() FM=
FM=![]() ,
,
∴FH=GH=HM=![]() ,
,
∵EF⊥GM,
∴GH=HM=![]() ,
,
∴EH=EF-FH=![]() ,
,
∵MH∥DE,
∴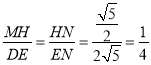 ,
,
∴EN=![]() ,
,
∴S△ENM=![]() ENMH=
ENMH=![]() .
.
故答案为:![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,![]() 的三个顶点的分别为
的三个顶点的分别为![]() ,
,![]() ,
,![]() (正方形网格中每个小正方形的边长是一个单位长度).
(正方形网格中每个小正方形的边长是一个单位长度).

(1)在网格内画出![]() 向下平移2个单位长度得到的
向下平移2个单位长度得到的![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(2)以点![]() 为位似中心,在网格内画出
为位似中心,在网格内画出![]() ,使
,使![]() 与
与![]() 位似,且位似比为
位似,且位似比为![]() ,点
,点![]() 的坐标是________;
的坐标是________;
(3)![]() 的面积是________平方单位.
的面积是________平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来佳木斯市旅游事业发展迅速,“大亮子河森林公园”“富锦国家湿地公园”“赫哲民族文化村”“大来岗达勒花海”等景区愈来愈为人们所知晓 . 在一次调查中,根据市民对这四个景区的了解情况,按答题分数分为![]() . 比较熟悉;
. 比较熟悉; ![]() . 基本了解;
. 基本了解; ![]() . 略有知晓;
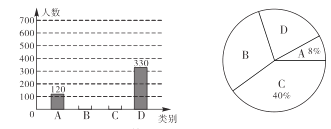
. 略有知晓; ![]() . 知之甚少,四类进行统计,绘制了以下两幅统计图(不完整),请根据图中信息解答以下各题:
. 知之甚少,四类进行统计,绘制了以下两幅统计图(不完整),请根据图中信息解答以下各题:
(1)本次调查活动的样本容量是 ;
(2)补全条形统计图;
(3)“略有知晓”类占扇形统计图的圆心角是多少度? “知之甚少”类市民占被调查人数的百分比是多少?
(4)已知某小区有 5000 人,那么估计对这些景区“比较熟悉”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△OAB在直角坐标系中的位置如图,点A在第一象限,点B在x轴正半轴上,OA=OB=6,∠AOB=30°.
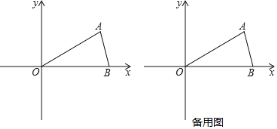
(1)求点A、B的坐标;
(2)开口向上的抛物线经过原点O和点B,设其顶点为E,当△OBE为等腰直角三角形时,求抛物线的解析式;
(3)设半径为2的⊙P与直线OA交于M、N两点,已知![]() ,P(m,2)(m>0),求m的值.
,P(m,2)(m>0),求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,则称
,则称![]() 与
与![]() 是关于
是关于![]() 的关联数.例如:若
的关联数.例如:若![]() ,则称
,则称![]() 与
与![]() 是关于2的关联数;
是关于2的关联数;
(1)若3与![]() 是关于5的关联数,求
是关于5的关联数,求![]() 的值
的值
(2)若![]() 与
与![]() 是关于4的关联数,求
是关于4的关联数,求![]() 的值.
的值.
(3)若![]() 与
与![]() 是关于
是关于![]() 的关联数,
的关联数, ![]() ,
,![]() 的值与
的值与![]() 无关,求
无关,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 在平面直角坐标系中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.
在平面直角坐标系中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.



(1)该抛物线的解析式为;
(2)如图1,Q为抛物线上位于直线AB上方的一动点(不与B、A重合),过Q作QP⊥x轴,交x轴于P,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;在此条件下,如图2,连接QN并延长,交y轴于E,连接AE,求t为何值时,MN∥AE.
(3)如图3,将直线AB绕点A顺时针旋转15度交抛物线对称轴于点C,点T为线段OA上的一动点(不与O、A重合),以点O为圆心、以OT为半径的圆弧与线段OC交于点D,以点A为圆心、以AT为半径的圆弧与线段AC交于点F,连接DF.在点T运动的过程中,四边形ODFA的面积有最大值还是有最小值?请求出该值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,弦
中,弦![]() 弦
弦![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
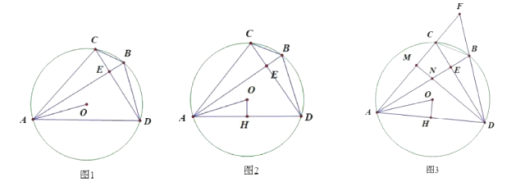
(1)求证:![]()
(2)如图2,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]()
(3)如图3,在(2)的条件下,延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】转转盘和摸球是等可能概率下的经典模型.
(1)在一个不透明的口袋中,放入除颜色外其余都相同的4个小球,其中1个白球,3个黑球搅匀后,随机同时摸出2个球,求摸出两个都是黑球的概率(要求釆用树状图或列表法求解);
(2)如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动2次,求指针2次都落在黑色区域的概率(要求采用树状图或列表法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
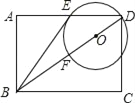
【题目】已知:如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD,BD分别交于点E、点F,且∠ABE=∠DBC.
(1)判断直线BE与⊙O的位置关系,并证明你的结论;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com