
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元(用列方程的方法解答);
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
【答案】
(1)
解:设去年A型车每辆x元,那么今年每辆(x+400)元,
根据题意得 ![]() ,
,
解之得x=1600,
经检验,x=1600是方程的解.
答:今年A型车每辆2000元
(2)
解:设今年7月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,
根据题意得50﹣m≤2m
解之得m≥ ![]() ,
,
∵y=(2000﹣1100)m+(2400﹣1400)(50﹣m)=﹣100m+50000,
∴y随m 的增大而减小,
∴当m=17时,可以获得最大利润.
答:进货方案是A型车17辆,B型车33辆
【解析】(1)设去年A型车每辆x元,那么今年每辆(x+400)元,列出方程即可解决问题.(2)设今年7月份进A型车m辆,则B型车(50﹣m)辆,获得的总利润为y元,先求出m的范围,构建一次函数,利用函数性质解决问题.本题考查一次函数的应用、分式方程等知识,解题的关键是设未知数列出方程解决问题,注意分式方程必须检验,学会构建一次函数,利用一次函数性质解决实际问题中的最值问题,属于中考常考题型.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖. 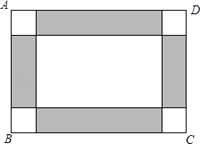
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点为B(2,1),且过点A(0,2),直线y=x与抛物线交于点D,E(点E在对称轴的右侧),抛物线的对称轴交直线y=x于点C,交x轴于点G,EF⊥x轴,垂足为F,点P在抛物线上,且位于对称轴的右侧,PQ⊥x轴,垂足为点Q,△PCQ为等边三角形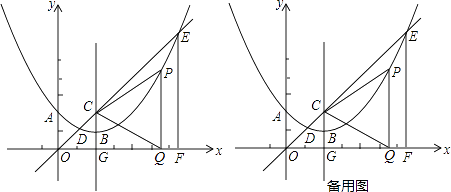
(1)求该抛物线的解析式;
(2)求点P的坐标;
(3)求证:CE=EF;
(4)连接PE,在x轴上点Q的右侧是否存在一点M,使△CQM与△CPE全等?若存在,试求出点M的坐标;若不存在,请说明理由.[注:3+2 ![]() =(
=( ![]() +1)2].
+1)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1,l2交于点C.
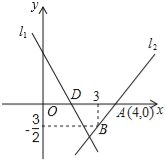
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在l2上存在异于点C的另一点P,使得△ADP与△ADC面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,埃航MS804客机失事后,国家主席亲自发电进行慰问,埃及政府出动了多艘舰船和飞机进行搜救,其中一艘潜艇在海面下500米的A点处测得俯角为45°的前下方海底有黑匣子信号发出,继续沿原方向直线航行2000米后到达B点,在B处测得俯角为60°的前下方海底有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).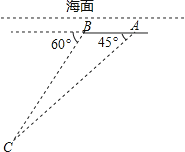
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,E、F两点分别在AB、AD上,CE与BF相交于G点.若∠EBG=25°,∠GCB=20°,∠AEG=95°,则∠A的度数为何?( ) 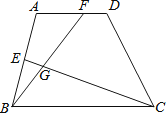
A.95
B.100
C.105
D.110
查看答案和解析>>
科目:初中数学 来源: 题型:
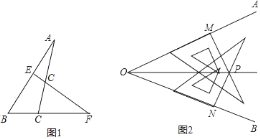
【题目】(1)如图1在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=45°,
∠F=30°,∠CGF=70°,求∠A的度数.
(2)利用三角板也能画出一个角的平分线,画法如下:①利用三角板在∠AOB的两边上分
别取OM=ON:②分别过点M、N画OM、ON的垂线,交点为![]() ;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.
;③画射线OP,所以射线OP为∠AOB的角平分线,请你评判这种作法的正确性并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①.AD=BC;②.DE=CF;③.BE∥AF.
⑴.请用其中两个关系式作为条件,另一个作为结论,写出所有正确的结论.
⑵.选择(1)中你写出的一个正确结论,说明它正确的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC; ②∠BCE+∠BCD=180°; ③AF2=EC2﹣EF2; ④BA+BC=2BF.其中正确的是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com