
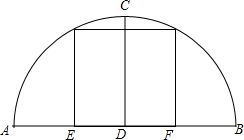
 如图为一圆弧形拱桥,桥下水面宽为AB=24米,拱顶高出水面CD=8米.现有一艘宽EF=8米,且船舱顶部为矩形的货船要经过这里,那么货船高出水面的部分最多不能超过多少米?
如图为一圆弧形拱桥,桥下水面宽为AB=24米,拱顶高出水面CD=8米.现有一艘宽EF=8米,且船舱顶部为矩形的货船要经过这里,那么货船高出水面的部分最多不能超过多少米? 分析 首先连接OA,设这座拱桥所在圆的半径为x米,由垂径定理,易得方程:x2=(x-8)2+122,解此方程即可求得半径;连接OM,由于MN=8米,可求得此时OH的高,即可求得OH-OD的长,即可得到结论.
解答 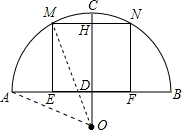 解:连接OA,
解:连接OA,
根据题意得:CD=8米,AB=24米,
则AD=$\frac{1}{2}$AB=12(米),
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC-CD=(x-8)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x-8)2+122,
解得:x=13,
连接OM,
∵MN=EF=8米,
∵OC⊥MN,
∴MH=$\frac{1}{2}$MN=4(米),
在Rt△OMH中,OH=$\sqrt{O{M}^{2}-M{H}^{2}}$=$\sqrt{105}$(米),
∵OD=OC-CD=13-8=5(米)
∵OH-OD=($\sqrt{105}$-5)米,
∴货船高出水面的部分最多不能超过($\sqrt{105}$-5)米.
点评 此题考查了垂径定理的应用.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.


科目:初中数学 来源: 题型:解答题
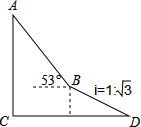 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | (-1,-1) | D. | (-2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知数轴甲上有A、B、C三点,分别表示-30、-20、0,动点M从点A出发,以每秒1个单位的速度向终点C移动,设点M移动的时间为t秒,点M在数轴甲上表示的数为m.
已知数轴甲上有A、B、C三点,分别表示-30、-20、0,动点M从点A出发,以每秒1个单位的速度向终点C移动,设点M移动的时间为t秒,点M在数轴甲上表示的数为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com