
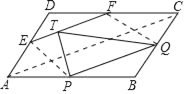
【题目】如图,在ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与ABCD的面积之比是______.

【答案】1:4
【解析】
如图,连接AC、PE、QF.设平行四边形ABCD的面积为8S,证明四边形EFQP是平行四边形,求出S平行四边形EFQP=4S和S△TPQ=2S即可解决问题.
解:如图,连接AC、PE、QF.设平行四边形ABCD的面积为8S.
∵DE=AE,DF=FC,
∴EF∥AC,EF:AC=1:2,
∴S△DEF=![]() S△DAC=
S△DAC=![]() ×4S=S,
×4S=S,
同理可证PQ∥AC,PQ:AC=1:2,S△CFQ=S△PQB=S△APE=S,
∴四边形EFQP是平行四边形,
∴S平行四边形EFQP=4S,
∴S△TPQ=![]() S平行四边形EFQP=2S,
S平行四边形EFQP=2S,
∴S△TPQ:S平行四边形ABCD=2S:8S=1:4,
故答案为1:4.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
![]()
(1)A、C两点间的距离是多少?
(2)在数轴上找到点D,使点D到B、C两点的距离相等;并在数轴上标出点D表示的数.
(3)若点E与B点的距离是5,求点E表示的数是什么?
(4)若点F与A点的距离是a(a>0),直接写出点F表示的数是多少?(用字母a表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,O是对角线AC、BD的交点,过点O作OE⊥OF,分别交AB、BC于E. F.

(1)求证:△OEF是等腰直角三角形。
(2)若AE=4,CF=3,求EF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个可以自由转动的均匀转盘A、B,分别被分成4等分和3等分,并在每份内均标有数字.小花为甲、乙两人设计了一个游戏规则如下:同时自由转动转盘A、B;两个转盘停止后,(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),将两个指针所指份内的两个数字相乘,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,则乙胜.但小强认为这样的规则是不公平的.
(1)请你用一种合适的方法(例如画树状图、列表)帮忙小强说明理由;
(2)请你设计一个公平的规则,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y1=mx的图象与反比例函数y2=![]() (m为常数,m≠0)的图象有一个交点的横坐标是2.
(m为常数,m≠0)的图象有一个交点的横坐标是2.
(1)求m的值;
(2)写出当y1<y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣2|+|﹣10|﹣|﹣5|
(2)(﹣3.5)+(+8![]() )﹣(﹣5.5)+(﹣2
)﹣(﹣5.5)+(﹣2![]() )
)
(3)﹣42+3×(﹣2)2×(![]() -1)÷(﹣1
-1)÷(﹣1![]() )
)
(4)(![]() ﹣
﹣![]() ﹣
﹣![]() )×(﹣24)+42÷(﹣2)3+(﹣1)2019
)×(﹣24)+42÷(﹣2)3+(﹣1)2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解(solution).已知:关于![]() 的方程
的方程![]() .
.
(1)若![]() 是方程
是方程![]() 的解,求
的解,求![]() 的值;
的值;
(2)若关于![]() 的方程
的方程![]() 的解比方程
的解比方程![]() 的解大6,求
的解大6,求![]() 的值;
的值;
(3)若关于![]() 的方程
的方程![]() 与
与![]() 均无解,求代数式
均无解,求代数式![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com