练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知：如图，在△ABC中，AB=AC，D在BC上，且DE∥AC交AB于E，点F在AC上，且DF=DC．求证：△EBD∽△DFC．
    考点：相似三角形的判定
    专题：证明题
    分析：利用“两角法”可以证得：△EBD∽△DFC．
    解答：证明：∵DE∥AC，
    ∴∠EDB=∠C．
    ∵AB=AC，
    ∴∠B=∠CFD．
    ∴△EBD∽△DFC．
    点评：本题考查了相似三角形的判定．
    （1）平行线法：平行于三角形的一边的直线与其他两边相交，所构成的三角形与原三角形相似；
    （2）三边法：三组对应边的比相等的两个三角形相似；
    （3）两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；
    （4）两角法：有两组角对应相等的两个三角形相似．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在半径为R的圆内有长为R的弦，则此弦所对的圆周角是（　　）
    A、30°
    B、60°
    C、30°或150°
    D、60°或120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    用代数式表示“比数a-3的绝对值的一半小10的数”，当a=7时，求出此数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解分式方程：
    1
    x-1
    -
    x
    x-1
    =1    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

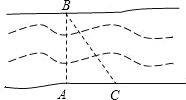    某高速公路工程需要测量某一条河的宽度．如图，一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向，测量员从A点开始沿岸边向正东方向前进100米到达点C处，测得∠ACB=60°．求所测之处河AB的宽度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在△ABC中，AB=AC，AB的垂直平分线与AC所在的直线相交所得锐角是50°．
    （1）请你根据题意画出图形；
    （2）试求出∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，圆心角120°的扇形OMN，绕着正六边形ABCDEF的中心O旋转，OM交AB于H，ON交CD于K，OM＞OA．
    （1）证明：△AOH≌△COK；
    （2）若AB=2，求正六边形ABCDEF与扇形OMN重叠部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一列火车匀速行驶，经过一条长300米的隧道需要20s的时间．隧道的顶上有一盏灯，垂直向下发光，灯光照在火车上的时间是10s．求这列火车的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）11-13+18                                 
    （2）-22×|-
    1
    2
    |+8÷(-2)2
    （3）24×(
    1
    6
    -
    3
    4
    -
    5
    8
    )+(-
    1
    3
    )2÷(-
    1
    72
    )        
    （4）
    1
    3
    (9a-3)-2(a+1)    ．

    查看答案和解析>>

    同步练习册答案