
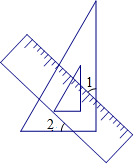
 将一个直角三角板和一把直尺如图放置,如果∠1=38°,则∠2的度数是52度.
将一个直角三角板和一把直尺如图放置,如果∠1=38°,则∠2的度数是52度.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
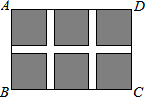 如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分钟花草,要使每一块花草的面积都为78cm2,那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )
如图,某小区规划在一个长30m、宽20m的长方形土地ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分钟花草,要使每一块花草的面积都为78cm2,那么通道宽应设计成多少m?设通道宽为xm,则由题意列得方程为( )| A. | (30-x)(20-x)=78 | B. | (30-2x)(20-2x)=78 | C. | (30-2x)(20-x)=6×78 | D. | (30-2x)(20-2x)=6×78 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{{x}^{2}+1}$ | B. | $\frac{x}{2x+1}$ | C. | $\frac{1}{{x}^{2}}$ | D. | $\frac{x-5}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com