
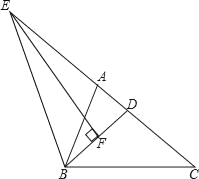
【题目】在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EAEC;
(2)若ED=6,BD=CD=3,求BC的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)根据EF是BD的垂直平分线,可得EB=ED,再证明△EAB∽△EBC,列比例式为![]() ,将EB与ED替换可得结论;
,将EB与ED替换可得结论;
(2)根据△EAB∽△EBC,得![]() ,代入可得EA=4,作高线AG、DH,根据勾股定理求EF=
,代入可得EA=4,作高线AG、DH,根据勾股定理求EF=![]() ,利用面积法可得DH的长,再用平行相似得:△AGE∽△DHE,列比例式得AG的长,从而得EG的长,根据勾股定理得BC的长.
,利用面积法可得DH的长,再用平行相似得:△AGE∽△DHE,列比例式得AG的长,从而得EG的长,根据勾股定理得BC的长.
详解:(1)证明:∵EF是BD的垂直平分线,
∴EB=ED,
∴∠EDB=∠EBD,
∵∠EDB=∠C+∠DBC,∠EBD=∠ABE+∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=∠ABE,
∵∠BEC=∠BEA,
∴△EAB∽△EBC,
∴![]() ,
,
∴EB2=EAEC,
∵EB=ED,
∴ED2=EAEC;
(2)∵ED=EB=6,BD=CD=3,
∴EC=6+3=9,
由(1)知:△EAB∽△EBC,
∴![]() ,
,
∴![]() ,EA=4,
,EA=4,
过A作AG⊥EB于G,过D作DH⊥EB于H,
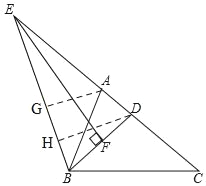
Rt△EFD中,ED=6,DF=![]() ,
,
∴EF=![]() ,
,
∴S△EBD=![]() EBDH=
EBDH=![]() BDEF,
BDEF,
∴DH=![]() EF=
EF=![]() ,
,
∵AG∥DH,
∴△AGE∽△DHE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理得:EG=![]() ,
,
∴BG=6﹣![]() =
=![]() ,
,
由勾股定理得:AB=![]() ,
,
∵△EAB∽△EBC,
∴![]() ,
,
∴![]() ,
,
∴BC=![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某九年级制学校围绕“每天30分钟的大课间,你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,点D、E分别在边BC、AC上,且AE=CD,AD与BE相交于点F.则∠BFD的度数为( )

A. 45° B. 90° C. 60° D. 30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com