
”¾ĢāÄæ”æŅŃÖŖA£¬BĮ½µŲĻą¾ą50Ē§Ć×£¬Ä³ČÕĻĀĪē¼×”¢ŅŅĮ½ČĖ·Ö±šĘļ×ŌŠŠ³µŗĶĘļĦĶŠ³µ“ÓAµŲ³ö·¢Ź»ĶłBµŲČēĶ¼ĖłŹ¾£¬Ķ¼ÖŠµÄÕŪĻßPQRŗĶĻ߶ĪMN·Ö±š±ķŹ¾¼×”¢ŅŅĮ½ČĖĖłŠŠŹ»µÄĀ·³ĢS£ØĒ§Ć×£©ÓėøĆČÕĻĀĪēŹ±¼ät£ØŹ±£©Ö®¼äµÄ¹ŲĻµ£®Ēėøł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ö±½ÓŠ“³ö£ŗ¼×Ęļ×ŌŠŠ³µ³ö·¢”” ””Š”Ź±ŗó£¬ŅŅĘļĦĶŠ³µ²ÅæŖŹ¼³ö·¢£»ŅŅĘļĦĶŠ³µ±Č¼×Ęļ×ŌŠŠ³µĢįĒ°”” ””Š”Ź±Ļȵ½“ļBµŲ£»
£Ø2£©Ēó³öŅŅĘļĦĶŠ³µµÄŠŠŹ»ĖŁ¶Č£»¼×Ęļ×ŌŠŠ³µŌŚĻĀĪē2Ź±ÖĮ5Ź±µÄŠŠŹ»ĖŁ¶Č£»
£Ø3£©µ±¼×”¢ŅŅĮ½ČĖĶ¾ÖŠĻąÓöŹ±£¬Ö±½ÓŠ“³öĻąÓöµŲÓėAµŲµÄ¾ąĄė£®

”¾“š°ø”æ£Ø1£©1£¬2£¬£»£Ø2£©ŅŅĘļĦĶŠµÄŠŠŹ»ĖŁ¶ČĪŖ50Ē§Ć×/Š”Ź±£»¼×Ęļ×ŌŠŠ³µŌŚĻĀĪē2Ź±ÖĮ5Ź±µÄŠŠŹ»ĖŁ¶Č10Ē§Ć×/Š”Ź±£¬£Ø3£©25Ē§Ć×£®
”¾½āĪö”æ
(1)ČĻÕę·ÖĪöĶ¼ĻóµĆµ½¼×±ČŅŅŌē³ö·¢µÄŹ±¼äÓėŅŅ±Č¼×Ōēµ½“ļµÄŹ±¼ä£»
(2)ĖŁ¶Č£½Ā·³Ģ”ĀŹ±¼ä£¬øł¾ŻĶ¼ĻóÖŠĢį¹©Źż¾Ż¼ĘĖć¼“æÉ£»
(3)¼×ŅŅĻąÓöŹ±¼“ŹĒOµćµÄĪ»ÖĆ£¬Éč“ĖŹ±ŅŅ³ö·¢ĮĖtŠ”Ź±£¬æÉĮŠ³ö¹ŲÓŚtµÄŅ»ŌŖŅ»“Ī·½³Ģ£¬“Ó¶ųĒó³öĻąÓöµŚÓėAµÄ¾ąĄė£®
(1)ÓÉĶ¼ĻóæÉÖŖ£ŗ¼×“Ó1Ź±æŖŹ¼³ö·¢£¬ŅŅ“Ó2Ź±æŖŹ¼³ö·¢£¬
2©1£½1£¬
¹Ź¼×Ęļ³µ³ö·¢1Š”Ź±ŗó£¬ŅŅĘļĦĶŠ³µ²ÅæŖŹ¼³ö·¢£¬
ÓÉĶ¼ĻóæÉÖŖ£ŗŅŅŌŚ3Ź±Ź±µ½“ļ£¬¼×ŌŚ5Ź±Ź±µ½“ļ£¬
5©3£½2£¬
¹ŹŅŅĘļĦĶŠ³µ±Č¼×Ęļ×ŌŠŠ³µĢįĒ°2Š”Ź±Ļȵ½“ļBµŲ£¬
¹Ź“š°øĪŖ£ŗ1£¬2£»
(2)ÓÉĶ¼ĻóæÉÖŖ£ŗŅŅµÄŠŠŹ»Ā·³ĢĪŖ50Ē§Ć×£¬Ź±¼äĪŖ3©2£½1Š”Ź±£¬
ŅŅĘļĦĶŠµÄŠŠŹ»ĖŁ¶ČĪŖ50”Ā1£½50Ē§Ć×/Š”Ź±£¬
¼×Ęļ×ŌŠŠ³µŌŚĻĀĪē2Ź±ÖĮ5Ź±µÄŠŠŹ»Ā·³ĢĪŖQ©RµÄ¾ąĄė£¬
50©20£½30Ē§Ć×£¬
Ź±¼äĪŖ5©2£½3Š”Ź±£¬
¼×Ęļ×ŌŠŠ³µŌŚĻĀĪē2Ź±ÖĮ5Ź±µÄŠŠŹ»ĖŁ¶ČĪŖ30”Ā3£½10Ē§Ć×/Š”Ź±£¬
“š£ŗŅŅĘļĦĶŠµÄŠŠŹ»ĖŁ¶ČĪŖ50Ē§Ć×/Š”Ź±£»¼×Ęļ×ŌŠŠ³µŌŚĻĀĪē2Ź±ÖĮ5Ź±µÄŠŠŹ»ĖŁ¶Č10Ē§Ć×/Š”Ź±£»
(3)ÉčĻąÓöŹ±ŅŅ³ö·¢ĮĖtŠ”Ź±£¬“ĖŹ±¶žÕߊŠŹ»¾ąĄėĻąĶ¬£¬
20+10t£½50t£¬
½āµĆ£ŗt£½0.5Š”Ź±£¬
“ĖŹ±¾ąĄėAµŲµÄ¾ąĄėĪŖŅŅµÄŠŠŹ»¾ąĄė50”Į0.5£½25Ē§Ć×£¬
“š£ŗµ±¼×”¢ŅŅĮ½ČĖĶ¾ÖŠĻąÓöŹ±£¬ĻąÓöµŲÓėAµŲµÄ¾ąĄėĪŖ25Ē§Ć×£¬
¹Ź“š°øĪŖ25Ē§Ć×£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ”°°²Č«½ĢÓż£¬¾ÆÖÓ³¤Ćł”±£¬ĪŖ“Ė£¬Ä³ÖŠŃ§×éÖÆČ«Š£1200Ćūѧɜ²Ī¼Ó°²Č«ÖŖŹ¶²āŹŌ£¬ĪŖĮĖ½ā±¾“Ī²āŹŌ³É¼ØµÄ·Ö²¼Ēéæö£¬“ÓÖŠĖ껜³éČ”ĮĖ²æ·ÖѧɜµÄ³É¼Ø£¬»ęÖĘ³öČēĻĀ²»ĶźÕūµÄĶ³¼ĘĶ¼±ķ£ŗ
·Ö¶ĪŹż | ʵŹż | ʵĀŹ |
60”Üx£¼70 | 30 | 0.15 |
70”Üx£¼80 | 60 | n |
80”Üx£¼90 | ||
90”Üx£¼100 | 20 | 0.1 |
ŗĻ¼Ę | m | 1 |
Ēėøł¾ŻŅŌÉĻĶ¼±ķĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±ķÖŠmµÄÖµĪŖ £¬ nµÄÖµĪŖ £»
£Ø2£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£»
£Ø3£©²āŹŌ³É¼ØµÄÖŠĪ»ŹżŌŚÄÄøö·ÖŹż¶Ī£æ
£Ø4£©¹ę¶Ø²āŹŌ³É¼Ø80·ÖŅŌÉĻ£Øŗ¬80·Ö£©ĪŖŗĻøń£¬Ēė¹Ą¼ĘČ«Š£Ń§ÉśÖŠŗĻøńČĖŹżŌ¼ĪŖ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖ½ųŠŠ±ČČüµÄĀ·³ĢÓėŹ±¼äµÄ¹ŲĻµČēĶ¼ĖłŹ¾£®
(1)ÕāŹĒŅ»³”________Ć×±ČČü£»
(2)Ē°Ņ»°ėČü³ĢÄŚ________µÄĖŁ¶Č½Ļæģ£¬×īÖÕ________Ó®µĆĮĖ±ČČü£»
(3)Į½ČĖµŚ________ĆėŌŚĶ¾ÖŠĻąÓö£¬ĻąÓöŹ±¾ąÖÕµć________Ć×£»
(4)¼×ŌŚĒ°8ĆėµÄĘ½¾łĖŁ¶ČŹĒ¶ąÉŁ£æ¼×ŌŚÕūøöČü³ĢµÄĘ½¾łĖŁ¶ČŹĒ¶ąÉŁ£æŅŅŌŚĒ°8ĆėµÄĘ½¾łĖŁ¶ČŹĒ¶ąÉŁ£æŅŅŌŚÕūøöČü³ĢµÄĘ½¾łĖŁ¶ČŹĒ¶ąÉŁ£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×£¬ŅŅĮ½ČĖŹĒNBAĮŖĆĖæ¶ūĢŲČĖ¶ÓµÄĮ½Ī»Ć÷ŠĒĒņŌ±£¬Į½ČĖŌŚĒ°ĪåøöČü¼¾µÄ·£Ēņ
ĆüÖŠĀŹČēĻĀ±ķĖłŹ¾£ŗ
¼×ĒņŌ±µÄĆüÖŠĀŹ£Ø%£© | 87 | 86 | 83 | 85 | 79 |
ŅŅĒņŌ±µÄĆüÖŠĀŹ£Ø%£© | 87 | 85 | 84 | 80 | 84 |
£Ø1£©·Ö±šĒó³ö¼×£¬ŅŅĮ½Ī»ĒņŌ±ŌŚĒ°ĪåøöČü¼¾·£ĒņµÄĘ½¾łĆüÖŠĀŹ£»
£Ø2£©ŌŚÄ³³”±ČČüÖŠ£¬Ņņ¶Ō·½ĒņŌ±¼¼Źõ·ø¹ęŠčŅŖæ¶ūĢŲČĖ¶ÓŃ”ÅÉŅ»Ćū¶ÓŌ±½ųŠŠ·£Ēņ£¬ÄćČĻĪŖ¼×£¬ŅŅĮ½Ī»ĒņŌ±ĖĄ“·£ĒņøüŗĆ£æ£ØĒėĶعż¼ĘĖćĖµĆ÷ĄķÓÉ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«µČ±ß”÷ABCČʵćCĖ³Ź±ÕėŠż×Ŗ120µĆµ½ ![]() EDC£¬Į¬½ÓAD£¬BD£®
EDC£¬Į¬½ÓAD£¬BD£®
ŌņĻĀĮŠ½įĀŪ£ŗ
¢ŁAC=AD£»
¢ŚBD ![]() AC£»
AC£»
¢ŪĖıߊĪACEDŹĒĮāŠĪ£®
ĘäÖŠÕżČ·µÄøöŹżŹĒ( )
A.O
B.1
C.2
D.3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
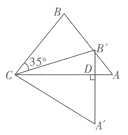
”¾ĢāÄæ”æČēĶ¼£¬°Ń ![]() ABCČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ35
ABCČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ35 ![]() £¬µĆµ½”÷
£¬µĆµ½”÷ ![]() £¬
£¬ ![]() ½»ACÓŚµćD£¬Čō
½»ACÓŚµćD£¬Čō ![]() £¬Ōņ
£¬Ōņ ![]() =
= ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
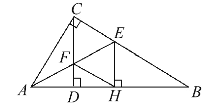
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() ÓŚ
ÓŚ![]() £¬
£¬![]() Ę½·Ö
Ę½·Ö![]() £¬·Ö±š½»
£¬·Ö±š½»![]() £¬
£¬![]() ÓŚ
ÓŚ![]() £¬
£¬![]() £¬
£¬![]() ÓŚ
ÓŚ![]() .Į¬½Ó
.Į¬½Ó![]() £¬ĒóÖ¤£ŗĖıߊĪ
£¬ĒóÖ¤£ŗĖıߊĪ![]() ŹĒĮāŠĪ.
ŹĒĮāŠĪ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¼×£¬Å×ĪļĻßy=x2-+bx+c½»xÖįÓŚµćA(-3£¬0)ŗĶµćB£¬½»yÖįÓŚµćC(0£¬3)£®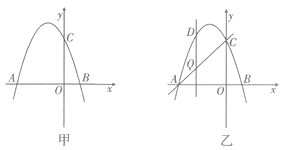
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČōµćPŌŚÅ×ĪļĻßÉĻ£¬ĒŅ ![]() £¬ĒóµćPµÄ×ų±ź£»
£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ČēĶ¼ŅŅ£¬ÉčµćQŹĒĻ߶ĪACÉĻµÄŅ»¶Æµć£¬×÷DQ ![]() xÖį£¬½»Å×ĪļĻßÓŚµćD£¬ĒóĻ߶ĪDQ³¤¶ČµÄ×ī“óÖµ£®
xÖį£¬½»Å×ĪļĻßÓŚµćD£¬ĒóĻ߶ĪDQ³¤¶ČµÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ2013ÄźŹĒŅ»øöČĆČĖ¼ĒŅäÓĢŠĀµÄÄź·Ż£¬Īķö²ĢģĘų³ÖŠųĮżÕÖĪŅ¹ś“ó²æ·ÖµŲĒų£¬æŚÕÖŹŠ³”³öĻÖČČĻś£¬Ä³Ęģ½¢ĶųµźÓĆ8000ŌŖ¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŠĶŗŵÄæŚÕÖ£¬ĻśŹŪĶźŗó¹²»ńĄū2800ŌŖ£¬½ų¼ŪŗĶŹŪ¼ŪČēĻĀ±ķ£ŗ
Ę·Ćū ¼Ūøń | ¼×ŠĶæŚÕÖ | ŅŅŠĶæŚÕÖ |
½ų¼Ū£ØŌŖ/“ü£© | 20 | 25 |
ŹŪ¼Ū£ØŌŖ/“ü£© | 26 | 35 |
£Ø1£©ĒóøĆĶųµź¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŠĶŗÅæŚÕÖø÷¶ąÉŁ“ü£æ
£Ø2£©øĆĶųµźµŚ¶ž“ĪŅŌŌ¼Ū¹ŗ½ų¼×”¢ŅŅĮ½ÖÖŠĶŗÅæŚÕÖ£¬¹ŗ½ųŅŅÖÖŠĶŗÅæŚÕÖ“üŹż²»±ä£¬¶ų¹ŗ½ų¼×ÖÖŠĶŗÅæŚÕÖ“üŹżŹĒµŚŅ»“ĪµÄ2±¶£®¼×ÖÖæŚÕÖ°“ŌŹŪ¼Ū³öŹŪ£¬¶ųŅŅÖÖæŚÕÖČĆĄūĻśŹŪ£®ČōĮ½ÖÖŠĶŗŵÄæŚÕÖ¶¼ŹŪĶź£¬ŅŖŹ¹µŚ¶ž“ĪĻśŹŪ»ī¶Æ»ńĄū²»ÉŁÓŚ3680ŌŖ£¬ŅŅÖÖŠĶŗŵÄæŚÕÖ×īµĶŹŪ¼ŪĪŖĆæ“ü¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com