
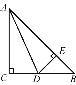
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是∠BAC的平分线,DE⊥AB,垂足为E.
(1)若CD=6![]() ,求AC的长;
,求AC的长;
(2)求证:AB-AC=CD.
【答案】(1)AC=BC=12+6![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由∠C=90°,AD是∠BAC的角平分线,DE⊥AB,根据角平分线的性质,即可得CD=DE,又由在△ABC中,AC=BC,∠C=90°,根据等腰三角形的性质,可求得AC=BC,∠B=45°,然后利用勾股定理,即可求得AC的长;
(2)首先证得AC=AE,又由(1)易得CD=DE=BE,然后利用线段的和差关系与等量代换的知识,即可求得AB-AC=CD.
(1)∵∠C=90°,AD是∠BAC的角平分线,DE⊥AB,
∴DE=CD=6![]() ,
,
∵在△ABC中,AC=BC,∠C=90°,
∴∠CAB=∠B=45°,
∴∠EDB=∠B=45°,
在Rt△BDE中,由勾股定理得:BD=12
∴AC=BC=CD+BD=12+6![]() ;
;
(2)∵AD是∠BAC的角平分线,
∴∠CAD=∠EAD,
∵∠C=90°,
∴AC⊥BC,
∵DE⊥AB,
∴∠ADC=∠ADE,
又∵AD=AD,
∴△ADC≌△ADE,
∴AE=AC,
∵CD=DE,DE=BE,
∴CD=BE,
∴AB-AC=AB-AE=BE=CD,
即:AB-AC=CD.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ=( )
A.60°
B.65°
C.72°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别是AB、CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;
(2)如图2,若∠P=∠PFD-∠BEP,求证:AB∥CD;
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
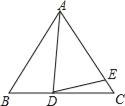
【题目】已知△ABC,AB=AC,D为BC上一点,E为AC上一点,AD=AE.
(1)如果∠BAD=10°,∠DAE=30°,那么∠EDC= °.
(2)如果∠ABC=60°,∠ADE=70°,那么∠BAD= °,∠CDE= °.
(3)设∠BAD=α,∠CDE=β猜想α,β之间的关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有【 】个.

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com