
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,D是劣弧![]() 的中点BD交AC于点E.
的中点BD交AC于点E.
(1)求证:AD2=DEDB.
(2)若BC=5,CD=![]() ,求DE的长.
,求DE的长.

【答案】(1)详见解析;(2)DE=![]() .
.
【解析】
(1)根据D是劣弧![]() 的中点,有∠DAC=∠ABD,结合公共角∠ADB,证明△ABD∽△EAD列出比例式即可;
的中点,有∠DAC=∠ABD,结合公共角∠ADB,证明△ABD∽△EAD列出比例式即可;
(2)根据D是劣弧![]() 的中点,有AD=CD,故DC2=DEDB,然后由BC是直径,可得△BCD是直角三角形,利用勾股定理求出BD的长即可解决问题.
的中点,有AD=CD,故DC2=DEDB,然后由BC是直径,可得△BCD是直角三角形,利用勾股定理求出BD的长即可解决问题.
(1)证明:∵D是劣弧![]() 的中点,
的中点,
∴![]() ,
,
∴∠ABD=∠DAC,
又∵∠ADB=∠EDA,
∴△ABD∽△EAD,
∴![]() =
=![]() ,
,
∴AD2=DEDB;
(2)解:由D是劣弧![]() 的中点,得AD=DC,则DC2=DEDB,
的中点,得AD=DC,则DC2=DEDB,
∵BC是直径,
∴△BCD是直角三角形,
∴BD=![]() =
=![]() =2
=2![]() ,
,
由DC2=DEDB得:(![]() )2=2
)2=2![]() DE,
DE,
解得:DE=![]() .
.


科目:初中数学 来源: 题型:
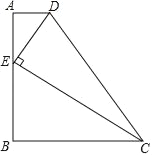
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点 M 满足横、纵坐标都为整数,则把点 M 叫做“整点”.例如:P(1,0)、Q(2,-2)都是“整点”.抛物线 y=mx2-2mx+m-1(m>0)与 x 轴交于 A、 B 两点,若该抛物线在 A、B 之间的部分与线段 AB 所围成的区域(包括边界)恰有 6 个整点,则 m 的取值范围是( )
A.![]() m
m ![]() B.
B.![]() m
m ![]() C.
C.![]() m
m ![]() D.
D.![]() m
m ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图坐标系中,O(0,0),A(6,6![]() ),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
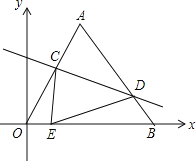
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中数学 来源: 题型:
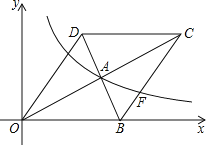
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是_____.
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(3,4),则点F的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,0),经过A点的直线交抛物线于点D (2, 3).
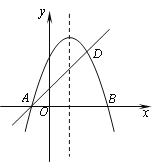
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点E (a,0) 作直线EF∥AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )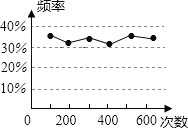
A. 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B. 掷一枚质地均匀的硬币,正面朝上的概率
C. 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D. 任意买一张电影票,座位号是2的倍数的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a<0)经过A(2,4)、B(﹣1,1)两点,顶点坐标为(h,k),则下列正确结论的序号是 .
①b>1;②c>2;③h<![]() ;④k≤1
;④k≤1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com