
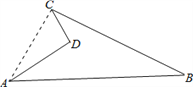
【题目】如图所示的一块地,∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m,求这块地的面积.

【答案】这块土地的面积为24m2
【解析】连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
解:连接AC.
在Rt△ACD中,AD=4,CD=3,
∴AC 2 =AD 2 +CD 2 =4 2 +3 2 =25,
又∵AC>0,
∴AC=5.
又∵BC=12,AB=13,
∴AC 2 +BC 2 =5 2 +12 2 =169,
又∵AB 2 =169,
∴AC 2 +BC 2 =AB 2 ,
∴△ACB是直角三角形,
∴S =S △ABC -S △ADC =30-6=24m2.
“点睛”考查了直角三角形面积公式以及勾股定理的应用,作辅助线是解决本题的关键.


科目:初中数学 来源: 题型:
【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中x1 , x2 , x3分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),则有( ) 
A.x1>x2>x3
B.x1>x3>x2
C.x2>x3>x1
D.x3>x2>x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励居民节约用水,规定如下用水收费标准:每户每月的用水量不超过12吨(含12吨)时,水费按a元/吨收费;超过时,不超过12吨(含12吨)时,水费按a元/吨收费;超过时,不超过12吨的部分仍按a元/吨收费,超过的部分按b元/吨(b>a)收费,已知该市小明家今年3月份和4月份的用水量、水费如表所示:
月份 | 用水量(立方米) | 水费(元) |
3 | 28 | 56 |
4 | 20 | 35.2 |
(1)求a,b的值;
(2)设某户1个月的用水量为x(吨),应交水费y(元),求出y与x之间的函数关系式;
(3)已知某户5月份的用水量为18吨,求该户5月份的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出那种方案的运费最省?最省是多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com