
ĄūĖâÄŋĄŋÉčĄũABCĢŽĩãPĘĮÆ―ÃæÄÚĩÄČÎŌâŌŧĩãĢĻAĄĒBĄĒCČýĩãģýÍâĢĐĢŽČôĩãPÓëĩãAĄĒBĄĒCÖÐČÎŌâÁ―ĩãĩÄÁŽÏßĩÄžÐ―ĮΊֹ―ĮĘąĢŽÔōģÆĩãPΊĄũABCĩÄŌŧļöđīđÉĩãĢŪ
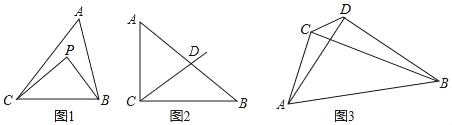
ĢĻ1ĢĐČįÍž1ĢŽČôĩãPĘĮĄũABCÄÚŌŧĩãĢŽĄÏAĢ―50ĄãĢŽĄÏACPĢ―10ĄãĢŽĄÏABPĢ―30ĄãĢŽĘÔËĩÃũĩãPĘĮĄũABCĩÄŌŧļöđīđÉĩãĢŪ
ĢĻ2ĢĐČįÍž2ĢŽRtĄũABCÖÐĢŽĄÏACBĢ―90ĄãĢŽACĢ―6ĢŽBCĢ―8ĢŽĩãDĘĮABĩÄÖÐĩãĢŽĩãPÔÚÉäÏßCDÉÏĢŽČôĩãPĘĮĄũABCĩÄđīđÉĩãĢŽÔōCPĢ―ĄĄ ĄĄĢŧ
ĢĻ3ĢĐČįÍž3ĢŽËÄąßÐÎABDCÖÐĢŽDBĢ―DAĢŽĄÏBCDĢ―45ĄãĢŽACĢ―![]() ĢŽCDĢ―3ĢŪÔōĩãDÄÜ·ņĘĮĄũABCĩÄđīđÉĩãĢŽČôÄÜĢŽĮóģöBCĩÄģĪĢšČôēŧÄÜĢŽĮëËĩÃũĀíÓÉĢŪ
ĢŽCDĢ―3ĢŪÔōĩãDÄÜ·ņĘĮĄũABCĩÄđīđÉĩãĢŽČôÄÜĢŽĮóģöBCĩÄģĪĢšČôēŧÄÜĢŽĮëËĩÃũĀíÓÉĢŪ
Ąūīð°ļĄŋ(1)žû―âÎöĢŧĢĻ2ĢĐ![]() ŧō
ŧō![]() ŧō10ĢŧĢĻ3ĢĐĩãDŋÉŌÔĘĮĄũABCĩÄđīđÉĩãĢŽBCĩÄģĪĘĮ
ŧō10ĢŧĢĻ3ĢĐĩãDŋÉŌÔĘĮĄũABCĩÄđīđÉĩãĢŽBCĩÄģĪĘĮ![]()
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝđīđÉĩãĩÄķĻŌåŋÉĩÃ―áÂÛĢŧ
ĢĻ2ĢĐČôĩãPĘĮĄũABCĩÄđīđÉĩãĢŽÓÐČýÖÖĮéŋöĢšĒŲĩąĄÏAPCĢ―90ĄãĘąĢŽĒÚĩąĄÏBPCĢ―90ĄãĘąĢŽĒÛĩąĄÏAPBĢ―90ĄãĘąĢŽ·ÖąðļųūÝSĄũACDĢ―![]() SĄũABCšÍÖą―ĮČý―ĮÐÎÐąąßÖÐÏßĩÄÐÔÖĘ―øÐОÆËãžīŋÉĢŧ
SĄũABCšÍÖą―ĮČý―ĮÐÎÐąąßÖÐÏßĩÄÐÔÖĘ―øÐОÆËãžīŋÉĢŧ
ĢĻ3ĢĐīæÔÚĢŽĩąĄÏADBĢ―90ĄãĘąĢŽĩãDĘĮĄũABCĩÄđīđÉĩãĢŽČįÍž5ĢŽŨũļĻÖúÏßĢŽđđ―ĻÖą―ĮČý―ĮÐÎĢŽÖĪÃũĄũAEDĄÕĄũDFBĢĻAASĢĐĢŽĩÃAEĢ―DFĢŽļųūÝĩČŅüÖą―ĮČý―ĮÐΞÆËãAEĩÄģĪĢŽŋÉĩÃDFĩÄģĪĢŽŋÉĩÃ―áÂÛĢŪ
ĢĻ1ĢХߥÏAĢ―50ĄãĢŽĄÏACPĢ―10ĄãĢŽĄÏABPĢ―30ĄãĢŽ
ĄāĄÏPCB+ĄÏPBCĢ―180ĄãĐ50ĄãĐ10ĄãĐ30ĄãĢ―90ĄãĢŽ
ĄāĄÏBPCĢ―90ĄãĢŽ
ĄāĩãPĘĮĄũABCĩÄŌŧļöđīđÉĩãĢŧ
ĢĻ2ĢĐĩãPÔÚÉäÏßCDÉÏĢŽČôĩãPĘĮĄũABCĩÄđīđÉĩãĢŽīæÔÚŌÔÏÂČýÖÖĮéŋöĢš
ĒŲČįÍž2ĢŽĩąĄÏAPCĢ―90ĄãĘąĢŽACĢ―6ĢŽBCĢ―8ĢŽ
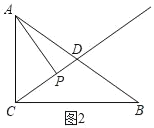
ĄāABĢ―10ĢŽ
ĄßDĘĮABĩÄÖÐĩãĢŽ
ĄāCDĢ―![]() ABĢ―5ĢŽ
ABĢ―5ĢŽ
SĄũACDĢ―![]() SĄũABCĢ―
SĄũABCĢ―![]() CDAPĢŽ
CDAPĢŽ
![]() ĢŽ
ĢŽ
APĢ―![]() ĢŽ
ĢŽ
Ąā Ģŧ
Ģŧ
ĒÚČįÍž3ĢŽĩąĄÏBPCĢ―90ĄãĘąĢŽ
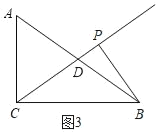
SĄũACDĢ―![]() SĄũABCĢ―
SĄũABCĢ―![]() CDBPĢŽ
CDBPĢŽ
![]() ĢŽ
ĢŽ
BPĢ―![]() ĢŽ
ĢŽ
ĄāCPĢ― Ģŧ
Ģŧ
ĒÛČįÍž4ĢŽĩąĄÏAPBĢ―90ĄãĘąĢŽ

ĄßDĘĮABĩÄÖÐĩãĢŽ
ĄāPDĢ―![]() ABĢ―5ĢŽ
ABĢ―5ĢŽ
ĄāPCĢ―5+5Ģ―10ĢŽ
ŨÛÉÏĢŽPCĩÄģĪĘĮ![]() ŧō
ŧō![]() ŧō10Ģŧ
ŧō10Ģŧ
đĘīð°ļΊĢš![]() ŧō
ŧō![]() ŧō10Ģŧ
ŧō10Ģŧ
ĢĻ3ĢĐīæÔÚĢŽ
ĩąĄÏADBĢ―90ĄãĘąĢŽĩãDĘĮĄũABCĩÄđīđÉĩãĢŽČįÍž5ĢŽđýAŨũAEĄÍCDĢŽ―ŧÖąÏßCDÓÚEĢŽđýBŨũBFĄÍCDÓÚFĢŽ
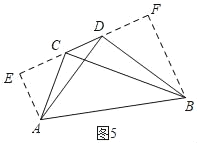
ĄßĄÏADBĢ―ĄÏADE+ĄÏBDFĢ―ĄÏBDF+ĄÏDBFĢ―90ĄãĢŽ
ĄāĄÏADEĢ―ĄÏDBFĢŽ
ĄßĄÏEĢ―ĄÏFĢ―90ĄãĢŽADĢ―BDĢŽ
ĄāĄũAEDĄÕĄũDFBĢĻAASĢĐĢŽ
ĄāAEĢ―DFĢŽ
ĄßADĢ―BDĢŽ
ĄāĄũADBĘĮĩČŅüÖą―ĮČý―ĮÐÎĢŽ
ĄāĄÏDABĢ―45ĄãĢŽ
ĄßĄÏBCDĢ―45ĄãĢŽ
ĄāĄÏBCDĢ―ĄÏDABĢŽ
ĄāAĄĒBĄĒDĄĒCËÄĩãđēÔēĢŽ
ĄāĄÏACBĢ―ĄÏADBĢ―90ĄãĢŽ
ĄāĄÏACEĢ―45ĄãĢŽ
ĄßACĢ―![]() ĢŽ
ĢŽ
ĄāAEĢ―CEĢ―DFĢ―![]() ĢŽ
ĢŽ
ĄāCF![]() ĢŽ
ĢŽ
ĄāBCĢ―![]() CEĢ―
CEĢ―![]() Ģŧ
Ģŧ
ŨÛÉÏĢŽĩãDŋÉŌÔĘĮĄũABCĩÄđīđÉĩãĢŽBCĩÄģĪĘĮ![]() ĢŪ
ĢŪ


 ÍŽē―Á·Ï°šÓÄÏīóŅ§ģö°æÉįÏĩÁÐīð°ļ
ÍŽē―Á·Ï°šÓÄÏīóŅ§ģö°æÉįÏĩÁÐīð°ļ ÍŽē―Á·Ï°ÎũÄÏĘĶ·ķīóŅ§ģö°æÉįÏĩÁÐīð°ļ
ÍŽē―Á·Ï°ÎũÄÏĘĶ·ķīóŅ§ģö°æÉįÏĩÁÐīð°ļ ēđģäÏ°Ėâ―ËÕÏĩÁÐīð°ļ
ēđģäÏ°Ėâ―ËÕÏĩÁÐīð°ļ Ņ§Á·ŋėģĩĩĀŋÚËãÐÄËãËŲËãĖėĖėÁ·ÏĩÁÐīð°ļ
Ņ§Á·ŋėģĩĩĀŋÚËãÐÄËãËŲËãĖėĖėÁ·ÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋžÆËãÄÜÁĶĘĮĘýŅ§ĩÄŧųąūÄÜÁĶĢŽÎŠÁË―øŌŧē―ÁË―âŅ§ÉúĩÄžÆËãĮéŋöĢŽģõ2020žķĘýŅ§ĀÏĘĶÃĮķÔÄģīÎŋžĘÔÖÐĩÚ19ĖâžÆËãĖâĩÄĩ÷ÖĮéŋö―øÐÐÁËĩũēéĢŽÏÖ·ÖąðīÓAĄĒBÁ―°āËæŧúļũģéČĄ10ÃûŅ§ÉúĩÄģÉžĻČįÏÂĢš
A°ā10ÃûŅ§ÉúĩÄģÉžĻŧæģÉÁËĖõÐÎÍģžÆÍžĢŽČįÏÂÍžĢŽ

B°ā10ÃûŅ§ÉúĩÄģÉžĻĢĻĩĨÎŧĢš·ÖĢĐ·ÖąðΊĢš9ĢŽ8ĢŽ9ĢŽ10ĢŽ9ĢŽ7ĢŽ9ĢŽ8ĢŽ10ĢŽ8
ūđýĀÏĘĶķÔËųģéČĄŅ§ÉúģÉžĻĩÄÕûĀíÓë·ÖÎöĢŽĩÃĩ―ÁËČįÏÂąíĘýūÝĢš
A°ā | B°ā | |
Æ―ūųĘý | 8.3 | a |
ÖÐÎŧĘý | b | 9 |
ÖÚĘý | 8ŧō10 | c |
žŦēî | 4 | 3 |
·―ēî | 1.81 | 0.81 |
ļųūÝŌÔÉÏÐÅÏĒĢŽ―âīðÏÂÁÐÎĘĖâĢŪ
ĢĻ1ĢĐēđČŦĖõÐÎÍģžÆÍžĢŧ
ĢĻ2ĢĐÖą―ÓÐīģöąíÖÐaĢŽbĢŽcĩÄÖĩĢšaĢ―ĄĄ ĄĄĢŽbĢ―ĄĄ ĄĄĢŽcĢ―ĄĄ ĄĄĢŧ
ĢĻ3ĢĐļųūÝŌÔÉÏĘýūÝĢŽÄãČÏΊAĄĒBÁ―ļö°āÄÄļö°āžÆËãĖâÕÆÎÕĩÃļüšÃĢŋĮëËĩÃũĀíÓÉĢĻÐīģöÆäÖÐÁ―ĖõžīŋÉĢĐĢšĄĄ ĄĄĢŪ
ĢĻ4ĢĐČô9·Öž°9·ÖŌÔÉÏΊÓÅÐãĢŽČôA°āđē55ČËĢŽÔōA°āžÆËãĖâÓÅÐãĩÄīóÔžÓÐķāÉŲČËĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔÚÆ―ÃæÖą―ĮŨøąęÏĩxOyÖÐĢŽÕý·―ÐÎABCDĩÄķĨĩã·ÖąðΊAĢĻ0ĢŽ4ĢĐĄĒBĢĻĐ4ĢŽ0ĢĐĄĒCĢĻ0ĢŽĐ4ĢĐĄĒDĢĻ4ĢŽ0ĢĐĢŽķÔÓÚÍžÐÎMĢŽļøģöČįÏÂķĻŌåĢšĩãPΊ͞ÐÎMÉÏČÎŌâŌŧĩãĢŽĩãQΊÕý·―ÐÎABCDąßÉÏČÎŌâŌŧĩãĢŽČįđûPĄĒQÁ―ĩãžäĩÄūāĀëÓÐŨîīóÖĩĢŽÄĮÃīģÆÕâļöŨîīóÖĩΊ͞ÐÎMĩÄĄ°Õý·―ūāĄąĢŽžĮŨũdĢĻMĢĐĢŪ
ĢĻ1ĢĐŌŅÖŠĩãEĢĻ0ĢŽ2ĢĐĢŽGĢĻĐ1ĢŽĐ1ĢĐĢŪ
ĒŲČįÍž1ĢŽÖą―ÓÐīģödĢĻĩãEĢĐĢŽdĢĻĩãGĢĐĩÄÖĩĢŧ
ĒÚČįÍž2ĢŽÉČÐÎEOFÔēÐÄ―ĮĄÏEOF=45ĄãĢŽ―ŦÉČÐÎEOFČÆĩãOËģĘąÕëÐýŨŠĶÁ―ĮĢĻ0ĢžĶÁĢž180ĄãĢĐĩÃĩ―ÉČÐÎE'OF'ĢŽĩądĢĻÉČÐÎE'OF'ĢĐČĄŨîīóÖĩĘąĢŽĮóĶÁ―ĮĩÄČĄÖĩ·ķΧĢŧ
ĢĻ2ĢĐĩãPÎŠÆ―ÃæÄÚŌŧķŊĩãĢŽĮŌÂúŨãdĢĻĩãPĢĐ=6ĢŽÖą―ÓÐīģöOPģĪķČĩÄČĄÖĩ·ķΧĢŪ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠĢšČįÍžĢŽūØÐÎABCDÖÐĢŽABĢ―2cmĢŽADĢ―3cmĢŪĩãPšÍĩãQÍŽĘąīÓĩãAģö·ĒĢŽĩãPŌÔ3cm/sĩÄËŲķČŅØAĄúD·―ÏōÔËķŊĩ―ĩãDΊÖđĢŽĩãQŌÔ2cm/sĩÄËŲķČŅØAĄúBĄúCĄúD·―ÏōÔËķŊĩ―ĩãDΊÖđĢŽÔōĄũAPQĩÄÃæŧýSĢĻcm2ĢĐÓëÔËķŊĘąžätĢĻsĢĐÖŪžäšŊĘýđØÏĩĩÄīóÖÂÍžÏóĘĮĢĻĄĄĄĄĢĐ
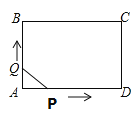
A. B.
B.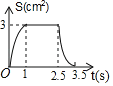
C. D.
D.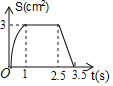
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÅŨÎïÏßyĢ―![]() x2+bx+cÓëxÖá―ŧÓÚAĢĻ4ĢŽ0ĢĐĄĒBĢĻĐ2ĢŽ0ĢĐĢŽÓëyÖá―ŧÓÚĩãCĢŪ
x2+bx+cÓëxÖá―ŧÓÚAĢĻ4ĢŽ0ĢĐĄĒBĢĻĐ2ĢŽ0ĢĐĢŽÓëyÖá―ŧÓÚĩãCĢŪ
ĢĻ1ĢĐĮóÅŨÎïÏßĩÄ―âÎöĘ―Ģŧ
ĢĻ2ĢĐĩãDΊĩÚËÄÏóÏÞÅŨÎïÏßÉÏŌŧĩãĢŽÉčĩãDĩÄšáŨøąęΊmĢŽËÄąßÐÎABCDĩÄÃæŧýΊSĢŽĮóSÓëmĩÄšŊĘýđØÏĩĘ―ĢŽēĒĮóSĩÄŨîÖĩĢŧ
ĢĻ3ĢĐĩãPÔÚÅŨÎïÏßĩÄķÔģÆÖáÉÏĢŽĮŌĄÏBPCĢ―45ĄãĢŽĮëÖą―ÓÐīģöĩãPĩÄŨøąęĢŪ
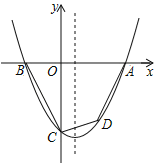
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
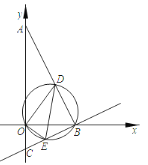
ĄūĖâÄŋĄŋČįÍžĢŽÔÚÆ―ÃæÖą―ĮŨøąęÏĩÖÐĢŽĄũABCĩÄķĨĩãÔÚŨøąęÖáÉÏĢŽAĢŽBĢŽCČýĩãĩÄŨøąę·ÖąðΊ (0ĢŽ2)ĢŽ(1ĢŽ0)ĢŽ(0ĢŽ-0ĢŪ5)ĢŽDΊÏßķÎABÉÏ-ļöķŊĩã(ēŧÓëĩãAĢŽBÖØšÏ)ĢŽđýBĢŽDĢŽ0ČýĩãĩÄÔēÓëÖąÏßBC―ŧÓÚĩãEĢŽĩąĄũOEDÃæŧýČĄĩÃŨîÐĄÖĩĘąĢŽEDĩÄģĪΊ________ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
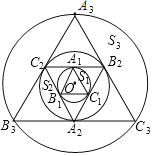
ĄūĖâÄŋĄŋČįÍžĢŽÐĄÔēOĩÄ°ëūķΊ1ĢŽĄũA1B1C1ĢŽĄũA2B2C2ĢŽĄũA3B3C3ĢŽĄĢŽĄũAnBnnŌĀīÎΊ͎ÐÄÔēOĩÄÄÚ―ÓÕýČý―ĮÐΚÍÍâĮÐÕýČý―ĮÐÎĢŽÓÉÏŌA1C1šÍŧĄA1C1ΧģÉĩÄđÐÎÃæŧýžĮΊS1ĢŽÓÉÏŌA2C2šÍŧĄA2C2ΧģÉĩÄđÐÎÃæŧýžĮΊS2ĢŽĄĢŽŌÔīËÏÂČĨĢŽÓÉÏŌAnnšÍŧĄAnnΧģÉĩÄđÐÎÃæŧýžĮΊSnĢŽÆäÖÐS2020ĩÄÃæŧýΊ_____ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠÔÚĄũABCÖÐĢŽAB=AC=5ĢŽBC=6ĢŽADĘĮBCąßÉÏĩÄÖÐÏßĢŽËÄąßÐÎADBEĘĮÆ―ÐÐËÄąßÐÎĢŪ
ĢĻ1ĢĐĮóÖĪĢšËÄąßÐÎADBEĘĮūØÐÎĢŧ
ĢĻ2ĢĐĮóūØÐÎADBEĩÄÃæŧýĢŪ
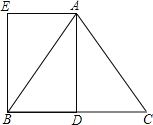
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
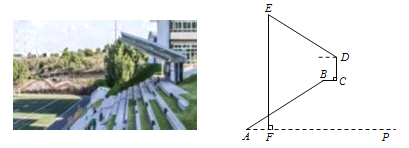
ĄūĖâÄŋĄŋČįÍžĘĮÄģŧ§ÍâŋīĖĻĩÄ―ØÃæÍžĢŽģĪ10mĩÄŋīĖĻABÓëËŪÆ―ĩØÃæAPĩÄžÐ―ĮΊ35ĄãĢŽÓëAPÆ―ÐÐĩÄÆ―ĖĻBCģĪΊ1.9mĢŽĩãFĘĮÕÚŅôÅïDEÉÏķËEÕýÏ·―ÔÚĩØÃæÉÏĩÄŌŧĩãĢŽēâĩÃAFĢ―2mĢŽÔÚĩē·įĮ―CDĩÄĩãDīĶēâĩÃĩãEĩÄŅö―ĮΊ26ĄãĢŽĮóÕÚŅôÅïDEĩÄģĪ. ĢĻēÎŋžĘýūÝĢšsin35ĄãĄÖ0.57ĢŽcos35ĄãĄÖ0.82ĢŽ sin26ĄãĄÖ0.44ĢŽcos26ĄãĄÖ0.90ĢĐ
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com