
【题目】小明同学要测量公园内被湖水隔开的两颗大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°的方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米;参考数据![]() ,
, ![]() ,
, ![]() ).
).
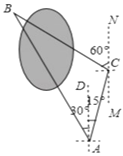
【答案】两棵大树A和B之间的距离约为386米
【解析】试题分析:(1)先利用平行线的性质得∠ACM=∠DAC=15°,再利用平角的定义计算出∠ACB=105°,然后根据三角形内角和计算∠ABC的度数;
(2)作CH⊥AB于H,如图,易得△ACH为等腰直角三角形,则AH=CH=![]() AC=100
AC=100![]() ,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=
,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=![]() CH=100
CH=100![]() ,AB=AH+BH=100
,AB=AH+BH=100![]() +100
+100![]() ,然后进行近似计算即可.
,然后进行近似计算即可.
试题解析:由题意可知:∠BAC=∠BAD+∠CAD=30°+15°=45°,∠MCA=∠CAD=15°,
∴∠ACB=180°-∠MCA-∠BCN=180°-15°-60°=105°
在△ABC中,∠ABC=180°-∠BCA-∠BAC=180°-105°-45°=30°;
从点C作CH⊥AB于点H
. 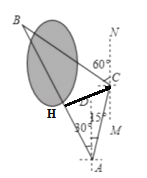
在Rt△ACH中,∵AC=200(米),∠CAH=45°,
∴CH=ACsin∠CAH=200×sin45°=200×![]() =100
=100![]() (米)
(米)
∴AH=CH=100![]() (米)
(米)
在Rt△BCH中,∵CH=100![]() (米),∠CBH=30°,
(米),∠CBH=30°,
∴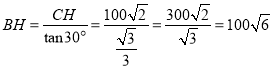 ;
;
∴AB=AH+BH=100![]() +100
+100![]() ≈386(米)
≈386(米)
答:两棵大树A和B之间的距离约为386米


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由. 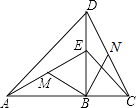
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3
B.∠1=∠2
C.∠2=∠3
D.∠1=∠2=∠3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车为市民出行带来了方便,某单车公司第一个月投放1000辆单车,计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三连个月投放单车数量的月平均增长率为x,则所列方程正确的是( )
A.1000(1+x)2=440B.1000(1+x)2=1000
C.1000(1+2x)=1000+440D.1000(1+x)2=1000+440
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.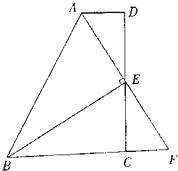
求证:
(1)FC=AD
(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
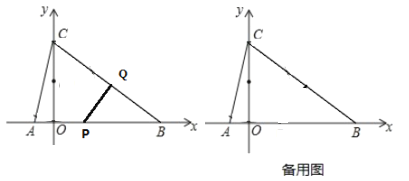
【题目】如图,在平面直角坐标系中,O是坐标原点,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
经过B,C两点,与x轴的另一个交点为点A,动点P从点A出发沿AB以每秒3个单位长度的速度向点B运动,运动时间为t(0<t<5)秒.
(1)求抛物线的解析式及点A的坐标;
(2)在点P从点A出发的同时,动点Q从点B出发沿BC以每秒3个单位长度的速度向点C运动,动点N从点C出发沿CA以每秒![]() 个单位长度的速度向点A运动,运动时间和点P相同.
个单位长度的速度向点A运动,运动时间和点P相同.
①记△BPQ的面积为S,当t为何值时,S最大,最大值是多少?
②是否存在△NCQ为直角三角形的情形?若存在,求出相应的t值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com