
分析 由tan∠B=$\frac{AD}{BD}$=$\frac{\sqrt{2}}{2}$可设AD=$\sqrt{2}$x,则BD=2x,在RT△ABD中根据勾股定理求得x的值,即可得BD、CD的长,分别求出点D在线段AB上和点D在线段AB延长线上时BC的长.
解答 解:∵tan∠B=$\frac{AD}{BD}$=$\frac{\sqrt{2}}{2}$,
∴设AD=$\sqrt{2}$x,则BD=2x,
∵AB2=AD2+BD2,
∴($\sqrt{6}$)2=($\sqrt{2}$x)2+(2x)2,
解得:x=1或x=-1(舍),
即BD=2,
又∵BD=2CD,
∴CD=1,
当点D在线段AB上时,如图1,
则BC=BD+CD=3;
当点D在线段AB延长线上时,如图2,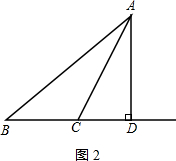
则BC=BD-CD=1;
故答案为:3或1.
点评 本题主要考查解直角三角形,熟练掌握直角三角形的边角、边边、角角间的关系式解直角三角形的基础,本题需考虑两种情况是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
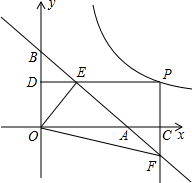 如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F
如图,已知直线y=-x+1与x轴交于A点,与y轴交于B点,P(a,b)为双曲线y=$\frac{1}{2x}$(x>0)上一动点,过P点分别作x轴、y轴的垂线,垂足分别为C、D,交直线AB于点E、F查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 3 | D. | 无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组邻边相等 | B. | 一组对边平行 | ||
| C. | 两组对边分别相等 | D. | 两组对边的和相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
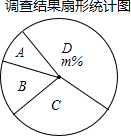 2016年3月8日,国务院批复同意自2016年起,将每年4月24日作为“中国航天日”,某市针对中学生开展了航天知识普及活动,活动结束后进行了一次航天知识问卷调查,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
2016年3月8日,国务院批复同意自2016年起,将每年4月24日作为“中国航天日”,某市针对中学生开展了航天知识普及活动,活动结束后进行了一次航天知识问卷调查,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.| 组别 | 成绩分组(单位:分) | 频数 | 频率 |
| A | 80≤x<85 | 100 | 0.1 |
| B | 85≤x<90 | 150 | |
| C | 90≤x<95 | 300 | c |
| D | 95≤x≤100 | a | |
| 合计 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
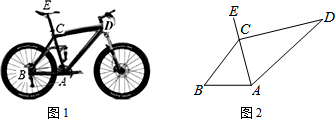
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
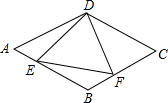 如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中:
如图,在菱形ABCD中,AB=6,∠A=60°,点E、F分别在AB,BC上,且AE=BF,下列结论中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com