
 如图,三个全等的等腰三角形按如图的形式(B、C、E、G在同一直线上)摆放,连接BF,已知腰长AB=$\sqrt{3}$,底边BC=1.
如图,三个全等的等腰三角形按如图的形式(B、C、E、G在同一直线上)摆放,连接BF,已知腰长AB=$\sqrt{3}$,底边BC=1.分析 (1)由条件可求得BG和FG的长,由等腰三角形的性质可求得∠ACB=∠FGC,可证得结论;
(2)如果问题较为浅显,可以提问求证:∠PCB=∠REC,这个问题只需要运用两直线平行,同位角相等进行解答.此题为发散性题型,不唯一.
解答 解:
(1)相似,理由如下:
∵△ABC≌△DCE≌△FEG
∴BC=CE=EG=1,
∴BG=2BC=3,FG=AB=$\sqrt{3}$
∴$\frac{BC}{FG}$=$\frac{1}{\sqrt{3}}$$\frac{\sqrt{3}}{3}$,$\frac{AC}{FG}$=$\frac{\sqrt{3}}{3}$,即$\frac{BC}{FG}$=$\frac{AC}{FG}$,
又∠ACB=∠FGB,
∴△ABC∽△BFG;
(2)A层问题(较浅显的,仅用到了1个知识点).
例如:①求证:∠PCB=∠REB.(或问∠PCB与∠REB是否相等)等;
②求证:PC∥RE,(或问线段PC与RE是否平行)等.
B层问题(有一定思考的,用到了2~3个知识点).
例如:①求证:∠BPC=∠BFG等,求证:BP=PR等;
②求证:△ABP∽△CQP等,求证:△BPC∽△BRE等;
③求证:△ABP∽△DQR等;④求BP:PF的值等.
A层解答举例:求证:PC∥RE
证明:△ABC≌△DCE
∴∠PCB=∠REB
∴PC∥RE
B层解答举例:求证:BP=PR
证明:∠ACB=∠REB,
∴AC∥DE.
又BC=CE,∴BP=PR.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,即①有两组角对应相等的三角形相似,②三边对应成比例的两个三角形相似,③两组边对应成比例且夹角相等的两个三角形相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | a-2<b-2 | B. | $-\frac{a}{5}<-\frac{b}{5}$ | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | 2a-1<2b-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
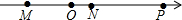 点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,那么表示数c的点为( )
点M,N,P和原点O在数轴上的位置如图所示,点M,N,P对应的有理数为a,b,c(对应顺序暂不确定).如果ab<0,a+b>0,那么表示数c的点为( )| A. | 点M | B. | 点N | C. | 点P | D. | 点O |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com