
 停止运动,△EFG也随之停止平移,设运动时间为x(s),FG的延长线交AC于H,(不考虑点P与G、F重合的情况)
停止运动,△EFG也随之停止平移,设运动时间为x(s),FG的延长线交AC于H,(不考虑点P与G、F重合的情况)| EG |
| AC |
| FG |
| BC |
| 4 |
| 8 |
| FG |
| 6 |
| ||
| 1 |
| 1 |
| 2 |
| 9+16 |
| EG |
| AH |
| EF |
| AF |
| FG |
| FH |
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 6 |
| 25 |
| 17 |
| 5 |
| 13 |
| 24 |
| 6 |
| 25 |
| 17 |
| 5 |
| 13 |
| 24 |
| 1 |
| 2 |
| 5 |
| 2 |
| 50 |
| 3 |
| 5 |
| 2 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
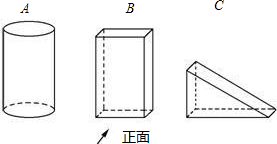 如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2,俯视图分别是A3、B3、C3.
如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2,俯视图分别是A3、B3、C3.
查看答案和解析>>
科目:初中数学 来源:2012届江苏省宜兴外国语学校九年级下期二模考试数学试卷(带解析) 题型:解答题
如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2;俯视图分别是A3、B3、C3.
(1)请你分别写出A1、A2、A3、B1、B2、B3、C1、C2、C3图形的名称;
(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A1、A2、A3的三张卡片放在甲口袋中,画有B1、B2、B3的三张卡片放在乙口袋中,画有C1、C2、C3的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.
① 通过画树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率;
② 小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜.这个游戏对双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省九年级下期二模考试数学试卷(解析版) 题型:解答题
如图所给的A、B、C三个几何体中,按箭头所示的方向为它们的正面,设A、B、C三个几何体的主视图分别是A1、B1、C1;左视图分别是A2、B2、C2;俯视图分别是A3、B3、C3.
(1)请你分别写出A1、A2、A3、B1、B2、B3、C1、C2、C3图形的名称;
(2)小刚先将这9个视图分别画在大小、形状完全相同的9张卡片上,并将画有A1、A2、A3的三张卡片放在甲口袋中,画有B1、B2、B3的三张卡片放在乙口袋中,画有C1、C2、C3的三张卡片放在丙口袋中,然后由小亮随机从这三个口袋中分别抽取一张卡片.
① 通过画树状图,求出小亮随机抽取的三张卡片上的图形名称都相同的概率;
② 小亮和小刚做游戏,游戏规则规定:在小亮随机抽取的三张卡片中只有两张卡片上的图形名称相同时,小刚获胜;三张卡片上的图形名称完全不同时,小亮获胜.这个游戏对双方公平吗?为什么?

查看答案和解析>>
科目:初中数学 来源:第9章《概率的简单应用》常考题集(01):9.1 抽签方法合理吗(解析版) 题型:解答题


查看答案和解析>>
科目:初中数学 来源:2008-2009学年九年级数学第三次月考测试卷(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com