
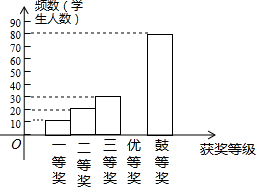
 为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
分析 (1)根据公式频率=频数÷样本总数,求得样本总数,再根据公式得出a,b的值即可;
(2)根据公式优胜奖对应的扇形圆心角的度数=优胜奖的频率×360°计算即可;
(3)利用总人数乘以对应的频率即可求解.
解答 解:(1):(1)样本总数为10÷0.05=200人,
a=200-10-20-30-80=60人,
b=30÷200=0.15,
故答案为60,0.15;
(2)优胜奖所在扇形的圆心角为0.30×360°=108°;
(3)16000×40%×(0.05+0.10)=960(人).
答:获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有960人.
点评 本题是一道利用统计知识解答实际问题的重点考题,主要考查利用统计图表,处理数据的能力和利用样本估计总体的思想.解答这类题目,观察图表要细致,对应的图例及其关系不能错位,计算要认真准确.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
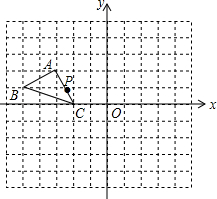 如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).
如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
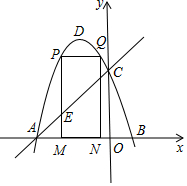 如图,抛物线y=-x2-2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2016B2017C2017的顶点B2017的坐标是(21008,21008).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2016B2017C2017的顶点B2017的坐标是(21008,21008).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com