
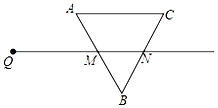
 如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2 cm,QM=4 cm.动点P从Q出发,沿射线QN以每秒1 cm的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径的⊙P与△ABC的AB边相切(切点在边上),则t值为2或6秒.
如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2 cm,QM=4 cm.动点P从Q出发,沿射线QN以每秒1 cm的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径的⊙P与△ABC的AB边相切(切点在边上),则t值为2或6秒. 分析 作PH⊥AB于H,如图,利用切线的性质得PH=$\sqrt{3}$,再利用等边三角形的性质和判定方法得到△BNM为等边三角形,则MN=BM=2,∠BMN=60°,接着在Rt△PMH中利用含30度的直角三角形三边的关系计算出PM=2,所以PQ=2,从而得到此时t=2s,同理当t=6时,⊙P与△ABC的AB边相切.
解答 解:作PH⊥AB于H,如图,
∵⊙P与△ABC的AB边相切,
∴PH=$\sqrt{3}$,
∵△ABC为等边三角形,MN∥AC,
∴△BNM为等边三角形,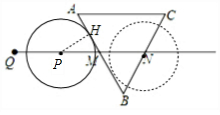
∴MN=BM=2,∠BMN=60°,
在Rt△PMH中,∵∠PMH=60°,
∴MH=$\frac{\sqrt{3}}{3}$PH=1,
∴PM=2HM=2,
∴PQ=QM-PM=4-2=2,
此时t=$\frac{2}{1}$=2(s),
同理当t=6时,⊙P与△ABC的AB边相切,
综上所述,当t为2或6秒时,⊙P与△ABC的AB边相切,
故答案为2或6.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了等边三角形的性质.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
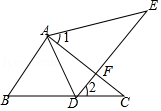 如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
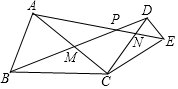 如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.
如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com