
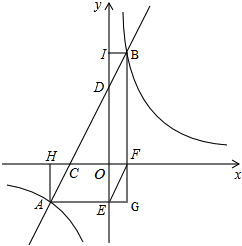
 ��ͼ��һֱ���뷴��������y=$\frac{k}{x}$��k��0������A��B���㣬ֱ����x�ᡢy��ֱ���C��D���㣬��A��B����ֱ���x�ᡢy�������ߣ�H��E��F��IΪ���㣬����EF���ӳ�AE��BF�ཻ�ڵ�G��
��ͼ��һֱ���뷴��������y=$\frac{k}{x}$��k��0������A��B���㣬ֱ����x�ᡢy��ֱ���C��D���㣬��A��B����ֱ���x�ᡢy�������ߣ�H��E��F��IΪ���㣬����EF���ӳ�AE��BF�ཻ�ڵ�G������ ��1�����ݷ�������������������Խ��м��㣻��2���ȸ��������ж���EGF�ס�AGB���ó���GAB=��GEF�������ж��ı���AEFC���ı���BDEF����ƽ���ı��Σ�������ƽ���ı��εĶԱ���ȵó����ۣ���3����B��������Ϊ��a��2a+2��������ֱ��������BDI�Ĺ��ɶ����г����̣����a��ֵ���ɵõ�B�����꣬�������뷴����������⣮
��� �⣺��1���ߵ�A��B���ڷ���������y=$\frac{k}{x}$��k��0����ͼ���ϣ�
��S����OFBI=S����OHAE=|k|=k��
�����OFBI�����OHAE�����֮��Ϊ2k��
��2����S����OFBI=S����OHAE=k��
��S����OEGF+S����OHAE=S����OFBI+S����OEGF
��S����AGFH=S����BIEG
��GA•GF=GE•GB
��$\frac{GE}{GA}=\frac{GF}{GB}$
�ߡ�EGF=��AGB
���EGF�ס�AGB
���GAB=��GEF
��EF��AB
��CF��AE��BF��DE
���ı���AEFC���ı���BDEF����ƽ���ı���
��AC=EF��BD=EF
��AC=BD
��3����ֱ��AB����ʽΪy=2x+2
��C��-1��0����D��0��2��
��CD=$\sqrt{5}$
��AB=2CD
��AC+BD=CD
�֡�AC=BD
��BD=$\frac{1}{2}$CD=$\frac{\sqrt{5}}{2}$
��B��������a��2a+2��
��ֱ��������BDI�У�BI=a��ID=2a+2-2=2a
��a2+��2a��2=��$\frac{\sqrt{5}}{2}$��2
���a1=$\frac{1}{2}$��a2=-$\frac{1}{2}$����ȥ��
��B��$\frac{1}{2}$��3��
��B��������뷴��������y=$\frac{k}{x}$����k=$\frac{3}{2}$
�෴���������Ľ���ʽΪ��y=$\frac{3}{2x}$
���� ������Ҫ�����˷�����������һ�κ����Ľ������⣬�������Ĺؼ������շ���������������������Լ�ƽ���ı��ε��ж�����������ʱע�⣬������������һ�κ����Ľ������꣬ͬʱ��������������ϵʽ����˿��Խ�B��������Ϊ��a��2a+2����ʹ������Ӽ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
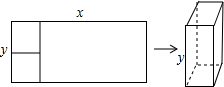 ��ͼ���ھ����н�ȡ������ͬ����������Ϊ��������ϡ��µ��棬ʣ��ľ���ǡ����Ϊ������IJ��棬��ԭ���εij��Ϳ��ֱ�Ϊx��y����y��x�ĺ���ͼ������ǣ�������
��ͼ���ھ����н�ȡ������ͬ����������Ϊ��������ϡ��µ��棬ʣ��ľ���ǡ����Ϊ������IJ��棬��ԭ���εij��Ϳ��ֱ�Ϊx��y����y��x�ĺ���ͼ������ǣ�������| A�� | 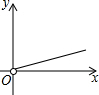 | B�� | 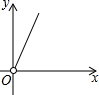 | C�� | 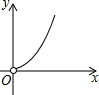 | D�� | 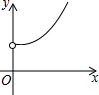 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
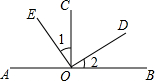 ��ͼ����A��O��B��һ��ֱ���ϣ���AOC=��BOC=90�㣬��1=��2����ͼ�л���Ľǹ���4�ԣ�
��ͼ����A��O��B��һ��ֱ���ϣ���AOC=��BOC=90�㣬��1=��2����ͼ�л���Ľǹ���4�ԣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{18}$ | B�� | -$\frac{1}{2}\sqrt{3}$ | C�� | $\frac{1}{\sqrt{2}}$ | D�� | $\sqrt{\frac{1}{5}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com