
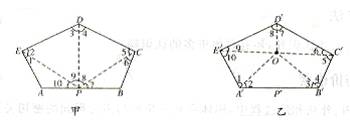
甲:在五边形ABCDE的边AB上取一点P,连结PC、PD、PE,则有
![]()
又∵![]() ,∴
,∴![]() ,
,
即![]() 。
。
乙:在五边形A′B′C′D′E′的内部任取一点O,连结OA′、OB′、OC′、OD′、OE′,则有(![]() A′O E′)+(
A′O E′)+(![]() A′O B′)+(
A′O B′)+(![]() B′O C′)+(
B′O C′)+(![]() C′O D′)+(
C′O D′)+(![]() D′O E′)=900
D′O E′)=900![]()
又∵![]() A′O E′+
A′O E′+![]() A′O B′+
A′O B′+![]() B′O C′+
B′O C′+![]() C′O D′+
C′O D′+![]() D′O E′=360
D′O E′=360![]() ,
,
∴![]() ,
,
即![]() E′A′B′+
E′A′B′+![]() A′B′C′+
A′B′C′+![]() B′C′D′+
B′C′D′+![]() C′D′E′+
C′D′E′+![]() D′E′A′=540
D′E′A′=540![]()
(1)填空:甲乙两位同学将 转化为 ,验证了 。
(2)假如将上述五边形换成n边形,请你分别依据甲、乙两位同学的思路方法验证n边形内角和公式![]() 。
。
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com