
 ��֪������ABCD��������CEFG��
��֪������ABCD��������CEFG������ ��1�����������ε����ʣ���Ȼ������BCG˳ʱ����ת90�㼴�ɵõ�������DCE���Ӷ��ж�����ֱ��֮��Ĺ�ϵ��
��2����������ε����ʣ�����SAS��Ȼ�ܹ��ж���BCG�ա�DCE���Ӷ�֤�����ۣ�
��3����ȫͼ����ͼ3����������ε����ʣ�����SAS��Ȼ�ܹ��ж���BCG�ա�DCE���Ӷ�֤�����ۣ�
��� �⣺��1��BG��DE��BG=DE��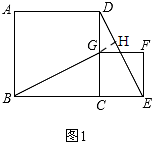
���ɣ���ͼ1�����ı���ABCD���ı���CEFG�������Σ�
��BC=DC��CG=CE����BCD=��ECG=90�㣬
���BCG=��DCE��
���BCG�ա�DCE��
��BG=DE����CBG=��CDE��
�֡ߡ�CBG+��BHC=90�㣬
���CDE+��DHG=90�㣬
��BG��DE��
��2��BG��DE��BG=DE��
���ɣ����ı���ABCD���ı���CEFG�������Σ�
��BC=DC��CG=CE����BCD=��ECG=90�㣬
���BCG=��DCE��
���BCG�ա�DCE��
��BG=DE����CBG=��CDE��
�֡ߡ�CBG+��BHC=90�㣬
���CDE+��DHG=90�㣬
��BG��DE��
��3��BG��DE��BG=DE��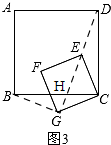
���ɣ���ͼ3�����ı���ABCD���ı���CEFG�������Σ�
��BC=DC��CG=CE����BCD=��ECG=90�㣬
���BCG=��DCE��
���BCG�ա�DCE��
��BG=DE����CBG=��CDE��
�֡ߡ�CBG+��BHC=90�㣬
���CDE+��DHG=90�㣬
��BG��DE��
���� �������ı����ۺ��⣬�����Ҫ������������ε��������ʣ�ע�����������е����������ε�Ӧ�ã���������Ρ����Ρ��������е������ε����߹�ϵ�����ù��ɶ�����⣬����������߽����ٶȺ�ȷ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-x=0�Ƕ���� | B�� | $\frac{x-1}{2}-\frac{x}{3}=4$�Ƿ�ʽ���� | ||
| C�� | $\sqrt{2}{x^2}-2x=\sqrt{3}$���������� | D�� | 2x2-y=4�Ƕ�Ԫ���η��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+y=-4 | B�� | 2x-y=-4 | C�� | 2x+y=4 | D�� | 2x-y=4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ��� | �Żݷ��� |
| AƷ������ | 150Ԫ/�� | ���� |
| BƷ������ | 100Ԫ/�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���D��BC�ߵ��е㣬��E��AD���е㣬��A����AF��BC���ҽ�CE���ӳ����ڵ�F������BF��
��ͼ���ڡ�ABC�У���D��BC�ߵ��е㣬��E��AD���е㣬��A����AF��BC���ҽ�CE���ӳ����ڵ�F������BF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x-1��y-1 | B�� | 3x��3y | C�� | -x��-y | D�� | $\frac{x}{2}��\frac{y}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ֱ�ǡ�ABC��ֱ�DZ߳���������MNPQ�ı߳���Ϊ10cm��AC��MN��ͬһֱ���ϣ���ʼʱA����M���غϣ��á�ABC�����˶������A����N���غϣ���д���ص��������y��cm2����MA����x��cm��֮��ĺ�����ϵʽ��ָ���Ա���ȡֵ��Χ����y=$\frac{1}{2}$x2 ��0��x��10������
��ͼ������ֱ�ǡ�ABC��ֱ�DZ߳���������MNPQ�ı߳���Ϊ10cm��AC��MN��ͬһֱ���ϣ���ʼʱA����M���غϣ��á�ABC�����˶������A����N���غϣ���д���ص��������y��cm2����MA����x��cm��֮��ĺ�����ϵʽ��ָ���Ա���ȡֵ��Χ����y=$\frac{1}{2}$x2 ��0��x��10�������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com