
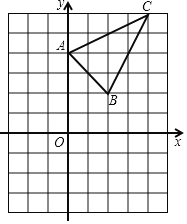
����Ŀ����ͼ����ABC������ƽ���ڣ��������������ֱ�ΪA��0��4����B��2��2����C��4��6���������������У�ÿ��С�����εı߳�Ϊ1��
��1��������ABC����ƽ��5����λ�õ��ġ�A1B1C1����д����B1�����ꣻ
��2���Ե�OΪλ�����ģ��ڵ�����������A2B2C2��ʹ��A2B2C2���ABCλ�ƣ���λ�Ʊ�Ϊ1��2��ֱ��д����C2������͡�A2B2C2�������
���𰸡���1������������2����3����
��2����������1.5.
��������
��1��ֱ������ƽ�Ƶ����ʵó���Ӧ��λ�ý����ó��𰸣�
��2��ֱ������λ��ͼ�ε����ʵó���Ӧ��λ�ý����������������ó��𰸣�
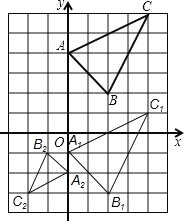
�⣺��1����ͼ��ʾ����A1B1C1����Ϊ����
��B1����������2����3����
��2����ͼ��ʾ����A2B2C2����Ϊ����
��C2������������2����3����
��A2B2C2�������4��![]() ��1��1��
��1��1��![]() ��1��2��
��1��2��![]() ��1��2��1.5��
��1��2��1.5��
 .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������A��5��![]() ����������y��ax2+bx�ĶԳ�����x��2����B����������x���һ�����㣬��C��y���ϣ���D�������ߵĶ��㣮
����������y��ax2+bx�ĶԳ�����x��2����B����������x���һ�����㣬��C��y���ϣ���D�������ߵĶ��㣮
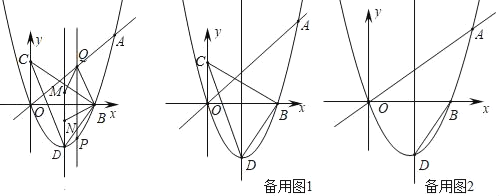
��1����a��b��ֵ��
��2������BCD��ֱ��������ʱ�����OBC�������
��3�����P��ֱ��OA�·�����������y��ax2+bx�ϣ���M��N�������ߵĶԳ����ϣ���M�ڵ�N���Ϸ�������MN��2������P��y���ƽ���߽�ֱ��OA�ڵ�Q����PQ���ʱ����ֱ��д���ı���BQMN���ܳ���Сʱ��Q��M��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����ABΪֱ������O�ֱ�BC��AC�ڵ�D��E������EB��OD�ڵ�F��
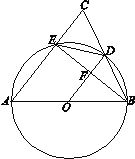
��1����֤��OD��BE��
��2����DE=![]() ��AB=
��AB=![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ƽ���ڣ�ֱ��![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() .������
.������![]() ������
������![]() ���
���![]() ������
������![]() �����һ������Ϊ
�����һ������Ϊ![]() .��
.��![]() �ڸ��������ϣ���λ��ֱ��
�ڸ��������ϣ���λ��ֱ��![]() ���Ϸ�.
���Ϸ�.
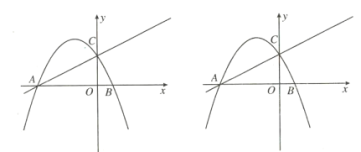
��1�������������ߵı���ʽ��
��2������![]() ��
��![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() �����
�����![]() �������
�������![]() �����֮��Ϊ
�����֮��Ϊ![]() ����
����![]() ������ֵ��
������ֵ��
��3������![]() ��
��![]() ��������
��������![]() ������
������![]() .��
.��![]() ��
��![]() ���ƣ����
���ƣ����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������![]() �ύ��
�ύ��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
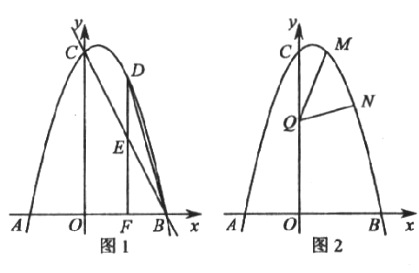
��1����������ߵı���ʽ����������ꣻ
��2������![]() ��
��![]() ���Ϸ��������ϵ�һ�����㣨���
���Ϸ��������ϵ�һ�����㣨���![]() ���غϣ�������
���غϣ�������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() .���
.���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() .
.
�����ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���
�ij���
��ֱ��![]() �ܷ��
�ܷ��![]() �ֳ����֮��Ϊ1��2�������֣����ܣ��������
�ֳ����֮��Ϊ1��2�������֣����ܣ��������![]() �����ꣻ�����ܣ���˵������.
�����ꣻ�����ܣ���˵������.
��3����ͼ2������![]() Ҳ�ڴ��������ϣ�����
Ҳ�ڴ��������ϣ�����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������ڣ���ֱ��д����
�������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȷֽǡ�����ѧʷ��һ�����������⣬�����ó߹治���ܡ����ȷֽǡ�����������ѧ������˹��������������һ�֡����ȷ���ǡ��ķ�������ͼ��������������ǡ�AOB����ֱ������ϵ�У���OB��x���ϡ���OA�뺯��![]() ��ͼ���ڵ�P����PΪԲ�ġ���2OPΪ�뾶������ͼ���ڵ�R���ֱ����P��R��x���y���ƽ���ߣ���ֱ���ཻ�ڵ�M������OM�õ���MOB�����MOB=
��ͼ���ڵ�P����PΪԲ�ġ���2OPΪ�뾶������ͼ���ڵ�R���ֱ����P��R��x���y���ƽ���ߣ���ֱ���ཻ�ڵ�M������OM�õ���MOB�����MOB=![]() ��AOB��Ҫ��������˹�ķ��������о��������⣺
��AOB��Ҫ��������˹�ķ��������о��������⣺
��1����P��![]() ��
��![]() ����R��
����R��![]() ��
��![]() ������ֱ��OM��Ӧ�ĺ�������ʽ���ú�
������ֱ��OM��Ӧ�ĺ�������ʽ���ú�![]() ��
��![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2���ֱ����P��R��y���x���ƽ���ߣ���ֱ���ཻ�ڵ�Q����˵��Q����ֱ��OM�ϣ����ݴ�֤����MOB=![]() ��AOB��
��AOB��
��3��Ӧ�����������õ��Ľ��ۣ���������ȷ�һ���۽ǣ������ּ�Ҫ˵����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����У�y����x�Ķ��κ�����( )
A. y��ax2+bx+c B. y��x(x��1)
C. y=![]() D. y��(x��1)2��x2
D. y��(x��1)2��x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ2��������ABCD����P�ӵ�A������ÿ��1����λ���ȵ��ٶ���A��D��C��·�����C�˶���ͬʱ��Q�ӵ�B������ÿ��2����λ���ȵ��ٶ���B��C��D��A��·�����A�˶�����Q�����յ�ʱ��Pֹͣ�ƶ������PQC�����ΪS���˶�ʱ��Ϊt�룬���ܴ��·�ӳS��t�ĺ�����ϵ��ͼ���ǣ�������
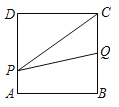
A.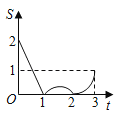 B.
B.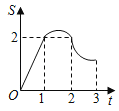
C.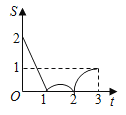 D.
D.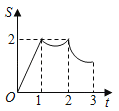
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
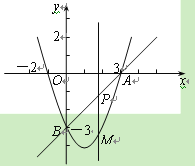
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��x2��mx��n������A(3��0)��
B(0����3)����P��ֱ��AB�ϵĶ��㣬����P��x��Ĵ������������ڵ�M�����P�ĺ�
����Ϊt��
(1)�ֱ����ֱ��AB�����������ߵĽ���ʽ��
(2)����P�ڵ������ޣ�����AM��BM�����߶�PM�ʱ������ABM�������
(3)�Ƿ���������ĵ�P��ʹ���Ե�P��M��B��OΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����P�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com