
【题目】如图,已知OE平分∠AOC,OF平分∠BOC 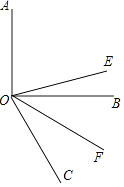
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数.
(2)若∠AOC=x°,∠EOF=y°,∠BOC=60°,请用x 的代数式来表示y.(直接写出结果就行).
【答案】
(1)解:∵∠AOB是直角,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=90°+60°=150°,
∵OE平分∠AOC,
∴∠EOC= ![]() ∠AOC=75°,
∠AOC=75°,
∵OF平分∠BOC,
∴∠COF= ![]() ∠BOC=30°,
∠BOC=30°,
∴∠EOF=∠EOC﹣∠COF=75°﹣30°=45°
(2)解:∵∠AOC=x°,OE平分∠AOC,
∴∠EOC= ![]() ∠AOC=
∠AOC= ![]() x°,
x°,
∵OF平分∠BOC,∠BOC=60°,
∴∠COF= ![]() ∠BOC=30°,
∠BOC=30°,
∴∠EOF=∠EOC﹣∠COF= ![]() x°﹣30°,即y=
x°﹣30°,即y= ![]() x﹣30
x﹣30
【解析】(1)由∠AOB是直角、∠BOC=60°知∠AOC=∠AOB+∠BOC=150°,根据OE平分∠AOC、OF平分∠BOC求得∠EOC、∠COF度数,由∠EOF=∠EOC﹣∠COF可得答案;(2)由∠AOC=x°,、OE平分∠AOC 知∠EOC= ![]() ∠AOC=
∠AOC= ![]() x°,由OF平分∠BOC、∠BOC=60°知∠COF=
x°,由OF平分∠BOC、∠BOC=60°知∠COF= ![]() ∠BOC=30°,根据∠EOF=∠EOC﹣∠COF可得答案.
∠BOC=30°,根据∠EOF=∠EOC﹣∠COF可得答案.
【考点精析】掌握角的平分线和角的运算是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列式子可以用“=”连接的是( )
A.5+4_______12-5
B.7+(-4)______7-(+4)
C.2+4(-2)______-12
D.2(3-4)_____23-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
查看答案和解析>>
科目:初中数学 来源: 题型:
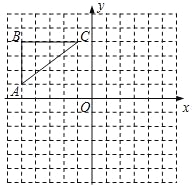
【题目】在正方形网格中,△ABC各顶点都在格点上,点A、C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2;
(3)点C1的坐标是 ;点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下 ![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得 ![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m﹣ ![]() ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
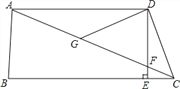
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.
(1)说明DC=DG;
(2)若DG=7,EC=4,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com