
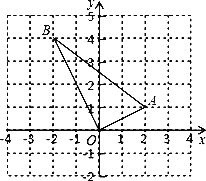
【题目】已知:如图,△OAB,点O为原点,点A、B的坐标分别是(2,1)、(﹣2,4).
(1)若点A、B都在一次函数y=kx+b图象上,求k,b的值;
(2)求△OAB的边AB上的中线的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
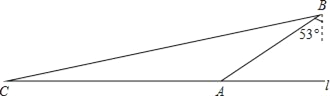
【题目】如图,在自动向西的公路l上有一检查站A,在观测点B的南偏西53°方向,检查站一工作人员家住在与观测点B的距离为7![]() km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈
km,位于点B南偏西76°方向的点C处,求工作人员家到检查站的距离AC.(参考数据:sin76°≈![]() ,cos76°≈
,cos76°≈![]() ,tan 76°≈4,sin53°≈
,tan 76°≈4,sin53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
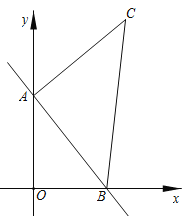
【题目】如图,一次函数![]() 的图像过点
的图像过点![]() 和点
和点![]() ,以线段
,以线段![]() 为边在第一象限内作等腰直角△ABC,使
为边在第一象限内作等腰直角△ABC,使![]()
(1)求一次函数的解析式;
(2)求出点![]() 的坐标
的坐标
(3)点![]() 是
是![]() 轴上一动点,当
轴上一动点,当![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
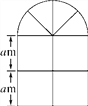
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
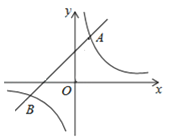
【题目】如图,已知在平面直角坐标系中, ![]() 是坐标原点,点A(2,5)在反比例函数
是坐标原点,点A(2,5)在反比例函数![]() 的图象上.一次函数
的图象上.一次函数![]() 的图象过点A,且与反比例函数图象的另一交点为B.
的图象过点A,且与反比例函数图象的另一交点为B.
(1)求![]() 和
和![]() 的值;
的值;
(2)设反比例函数值为![]() ,一次函数值为
,一次函数值为![]() ,求
,求![]() 时
时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1, ![]() )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.
(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年水果大丰收,A,B两个水果基地分别收获水果380件、320件,现需把这些水果全部运往甲、乙两销售点,从A基地运往甲、乙两销售点的费用分别为每件40元和20元,从B基地运往甲、乙两销售点的费用分别为每件15元和30元,现甲销售点需要水果400件,乙销售点需要水果300件.
(1)设从A基地运往甲销售点水果x件,总运费为W元,请用含x的代数式表示W,并写出x的取值范围;
(2)若总运费不超过18300元,且A地运往甲销售点的水果不低于200件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郊区某中学学霸父母只要有时间就陪孩子一起完成家庭作业,在某天晚上,勤芬准备完成作业时:化简(![]() x2+7x+6)﹣(7x+8x2﹣4).发现系数“
x2+7x+6)﹣(7x+8x2﹣4).发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)她把“![]() ”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
(2)爸爸说:“你猜错了,我看了标准答案的结果是常数.”请你通过计算说明来帮助勤芬得到原题中“![]() ”是几.
”是几.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com