
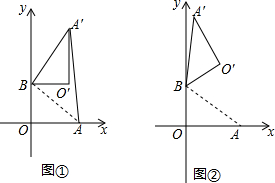
分析 (1)如图①,先利用勾股定理计算出AB=5,再根据旋转的性质得BA=BA′,∠ABA′=90°,则可判定△ABA′为等腰直角三角形,然后根据等腰直角三角形的性质求AA′的长;
(2)作O′H⊥y轴于H,如图②,利用旋转的性质得BO=BO′=3,∠OBO′=120°,则∠HBO′=60°,再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长,然后利用坐标的表示方法写出O′点的坐标;
(3)由旋转的性质得BP=BP′,则O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,易得O′P+BP=O′C,利用两点之间线段最短可判断此时O′P+BP的值最小,接着利用待定系数法求出直线O′C的解析式为y=$\frac{5\sqrt{3}}{3}$x-3,从而得到P($\frac{3\sqrt{3}}{5}$,0),则O′P′=OP=$\frac{3\sqrt{3}}{5}$,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.
解答 解:(1)如图①,
∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵△ABO绕点B逆时针旋转90°,得△A′BO′,
∴BA=BA′,∠ABA′=90°,
∴△ABA′为等腰直角三角形,
∴AA′=$\sqrt{2}$BA=5$\sqrt{2}$;
(2)作O′H⊥y轴于H,如图②,
∵△ABO绕点B逆时针旋转120°,得△A′BO′,
∴BO=BO′=3,∠OBO′=120°,
∴∠HBO′=60°,
在Rt△BHO′中,∵∠BO′H=90°-∠HBO′=30°,
∴BH=$\frac{1}{2}$BO′=$\frac{3}{2}$,O′H=$\sqrt{3}$BH=$\frac{3\sqrt{3}}{2}$,
∴OH=OB+BH=3+$\frac{3}{2}$=$\frac{9}{2}$,
∴O′点的坐标为($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$);
(3)∵△ABO绕点B逆时针旋转120°,得△A′BO′,点P的对应点为P′,
∴BP=BP′,
∴O′P+BP′=O′P+BP,
作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,
则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小,
∵点C与点B关于x轴对称,
∴C(0,-3),
设直线O′C的解析式为y=kx+b,
把O′($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$),C(0,-3)代入得$\left\{\begin{array}{l}{\frac{3\sqrt{3}}{2}k+b=\frac{9}{2}}\\{b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{5\sqrt{3}}{3}}\\{b=-3}\end{array}\right.$,
∴直线O′C的解析式为y=$\frac{5\sqrt{3}}{3}$x-3,
当y=0时,$\frac{5\sqrt{3}}{3}$x-3=0,解得x=$\frac{3\sqrt{3}}{5}$,则P($\frac{3\sqrt{3}}{5}$,0),
∴OP=$\frac{3\sqrt{3}}{5}$,
∴O′P′=OP=$\frac{3\sqrt{3}}{5}$,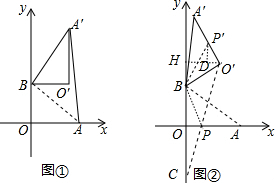
作P′D⊥O′H于D,
∵∠BO′A′=∠BOA=90°,∠BO′H=30°,
∴∠DP′O′=30°,
∴O′D=$\frac{1}{2}$O′P′=$\frac{3\sqrt{3}}{10}$,P′D=$\sqrt{3}$O′D=$\frac{9}{10}$,
∴DH=O′H-O′D=$\frac{3\sqrt{3}}{2}$-$\frac{3\sqrt{3}}{10}$=$\frac{6\sqrt{3}}{5}$,
∴P′点的坐标为($\frac{6\sqrt{3}}{5}$,$\frac{27}{5}$).
点评 本题考查了几何变换综合题:熟练掌握旋转的性质;理解坐标与图形性质;会利用两点之间线段最短解决最短路径问题;记住含30度的直角三角形三边的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
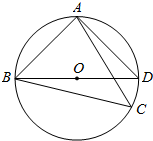 如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45°
如图,点C为△ABD的外接圆上的一动点(点C不在$\widehat{BAD}$上,且不与点B,D重合),∠ACB=∠ABD=45°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
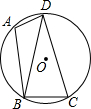 如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
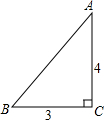 如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )
如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )| A. | c>a>b | B. | b>a>c | C. | c>b>a | D. | b>c>a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.
如图,在?ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.969×107 | B. | 9.69×107 | C. | 9.69×106 | D. | 969×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com