
【题目】在平面直角坐标系中,抛物线y=﹣![]() x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
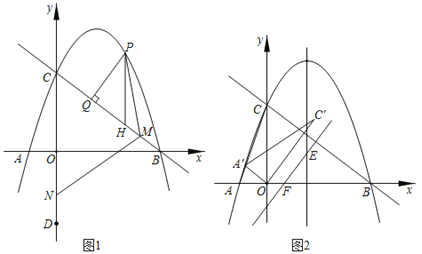
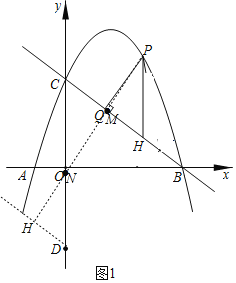
(1)如图1,点P为直线BC上方抛物线上一动点,过点P作PH∥y轴,交直线BC于点H,过点P作PQ⊥BC于点Q,当PQ﹣![]() PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+
PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+![]() ND的最小值;
ND的最小值;
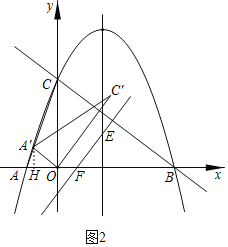
(2)如图2,连接AC,将△OAC绕着点O顺时针旋转,记旋转过程中的△OAC为△OA'C',点A的对应点为点A',点C的对应点为点C'.当点A'刚好落在线段AC上时,将△OA'C'沿着直线BC平移,在平移过程中,直线OC'与抛物线对称轴交于点E,与x轴交于点F,设点R是平面内任意一点,是否存在点R,使得以B、E、F、R为顶点的四边形是菱形?若存在,请直接写出点R的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,(
;(2)存在,(![]() ,10)或(
,10)或(![]() ,﹣
,﹣![]() )或(3,﹣
)或(3,﹣![]() )
)
【解析】
(1)PQ﹣![]() PH=PHsinα﹣PH=
PH=PHsinα﹣PH=![]() PH,当x=4时,PH最大,即PQ﹣
PH,当x=4时,PH最大,即PQ﹣![]() PH最大,此时点P(4,3);过点D作直线DH∥BC,则∠NDH=∠OBC,sin∠OCB=cos∠OBC=cosα=
PH最大,此时点P(4,3);过点D作直线DH∥BC,则∠NDH=∠OBC,sin∠OCB=cos∠OBC=cosα=![]() ,过点P作PH⊥DH于点H,则此时,PM+MN+
,过点P作PH⊥DH于点H,则此时,PM+MN+![]() ND的最小,即可求解;
ND的最小,即可求解;
(2)分BF是边、BF为对角线两种情况,分别求解即可.
解:(1)抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,
令x=0,则y=6;
令y=0,则![]() ,解得:
,解得:![]() ,
,![]() ;
;
∴点A、B、C的坐标分别为:(﹣2,0)、(8,0)、(0,6),
由点B、C的坐标得直线BC的表达式为:y=﹣![]() x+6,
x+6,
∴∠HPQ=∠OBC,则tan∠HPQ=tan∠OBC=![]() =tanα,
=tanα,
则sinα=![]() ,cos
,cos![]() ,
,
PQ﹣![]() PH=PHsinα﹣PH=
PH=PHsinα﹣PH=![]() PH,
PH,
而PH=y=![]() =
=![]() ,
,
当x=4时,PH最大,即PQ﹣![]() PH最大,
PH最大,
此时点P(4,3);
过点D作直线DH∥BC,则∠NDH=∠OBC,sin∠OCB=cos∠OBC=cosα=![]() ,
,
过点P作PH⊥DH于点H,则此时,PM+MN+![]() ND的最小,
ND的最小,
则HD=DNsin∠NDH=DNcosα=![]() ,
,
则PM+MN+![]() ND=PM+MN+HN=PH,即此时PM+MN+
ND=PM+MN+HN=PH,即此时PM+MN+![]() ND的最小,
ND的最小,
直线PH⊥HD,则直线PH表达式中的k值为:![]() ,
,
由k值和点P的坐标得:直线PH的表达式为:y=![]() x,故点N(0,0),
x,故点N(0,0),
HN=NDcosα=6×![]() =
=![]() ,PN=PO=5,
,PN=PO=5,
PH=5+![]() =
=![]() ,
,
即PM+MN+![]() ND的最小值为:
ND的最小值为:![]() ;
;
(2)OA=OA′=2,
过点A′作A′H⊥x轴于点H,tan∠A′AO=![]() =3=tanβ,
=3=tanβ,
设AH=x,则A′H=3x,OH=2﹣x,
由勾股定理得:22=(3x)2+(2﹣x)2,
解得:x=![]() ,故点A′(﹣
,故点A′(﹣![]() ,
,![]() ),
),
则直线OA′的表达式为:y=﹣![]() x,
x,
OA′⊥C′O,则直线OC′的表达式为:y=![]() x,
x,
设直线OC′向右平移了m个单位,则直线OC′的表达式为:y=![]() (x﹣m),
(x﹣m),
抛物线的对称轴为:x=3,
则点F(m,0),点E(3,4﹣![]() m),而点B(8,0);
m),而点B(8,0);
①当BF是边时,
则BF=ER=8﹣m,则点R(3+8﹣m,4﹣![]() m),
m),
由BR=FR得:(8﹣m)2=(3﹣m)2+(4﹣![]() m)2,
m)2,
解得:m=﹣![]() 或
或![]() ,
,
故点R(![]() ,10)或(
,10)或(![]() ,﹣
,﹣![]() );
);
②当BF为对角线时,
则点R(3,![]() m﹣4),
m﹣4),
由FR=BR得:(m﹣3)2+(![]() m﹣4)2=52+(
m﹣4)2=52+(![]() m﹣4)2,
m﹣4)2,
解得:m=8(舍去)或﹣2,
故点R(3,﹣![]() );
);
综上所述,点R的坐标为:(![]() ,10)或(
,10)或(![]() ,﹣
,﹣![]() )或(3,﹣
)或(3,﹣![]() ).
).


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
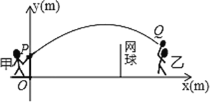
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲在O点正上方1 m的点P发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式:![]() ,已知点O与球网的水平距离为5 m,球网的高度1.55 m.
,已知点O与球网的水平距离为5 m,球网的高度1.55 m.
(1)当![]() 时,求h的值,并通过计算判断此球能否过网;
时,求h的值,并通过计算判断此球能否过网;
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() 的Q处时,乙扣球成功,求a的值.
的Q处时,乙扣球成功,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,![]() 是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
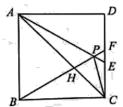
A.AE=2DEB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
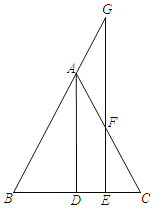
【题目】如图所示,在△ABC中,AB=AC,AD平分∠BAC,点G是BA延长线上一点,点F是AC上一点,AG=AF,连接GF并延长交BC于E.
(1)若∠B=55°,求∠AFG的度数;
(2)求证:GE⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元.每天可以销售
元.每天可以销售![]() 件,为尽快减少库存,商场决定降价促销.
件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件![]() 元,求两次下降的百分率;
元,求两次下降的百分率;
(2)经调查,若该商品每降价![]() 元,每天可多销售
元,每天可多销售![]() 件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?
件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
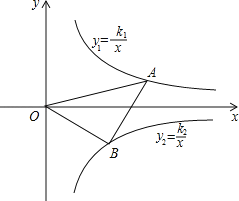
【题目】如图,在平面直角坐标系中,反比例函数y1=![]() (x>0)的图象与y2=
(x>0)的图象与y2=![]() (x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=
(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=![]() (x>0)和y2=
(x>0)和y2=![]() (x>0)的图象上.若OB=AB,点B的纵坐标为﹣2,则点A的坐标为_____.
(x>0)的图象上.若OB=AB,点B的纵坐标为﹣2,则点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
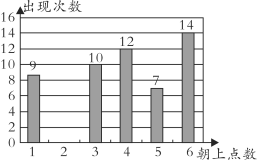
【题目】小强与小颖两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,共随机抛了60次,出现向上点数的次数如下图所示:
(1)请补全下边的统计图;
(2)小强说:“如果抛600次,则出现向上点数为3的次数正好是100次.”他的说法正确吗?为什么?
(3)若小强与小颖各随机抛一枚骰子,求两枚骰 子向上点数之和为3的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com