
如下图所示,AB为⊙O的直径,BC切⊙O于B,AC交⊙O于P,CE=BE,E在BC上.求证PE是⊙O的切线.

|
证明:连接OP,BP,∵AB为直径, ∴∠APB=∠BPC=90°, ∵CE=BE,∴EP=EB, ∴∠EBP=∠EPB, 又BC切⊙O于B,∴∠ABC=90°, ∴∠OBP+∠EBP=90°, ∵OB=OP,∴∠OBP=∠OPB, ∴∠OPB+∠EPB=90°,∴OP⊥EP, 又OP为⊙O的半径,∴PE是⊙O的切线. 分析:欲证PE是⊙O的切线,可连接OP,只需证OP⊥PE即可,∵AB为直径,故连接BP,可得∠APB=90°,∴PE=EB,∠EBP=∠EPB,又OB=OP,∴∠OBP=∠OPB,由∠ABC=90°,可得∠OPE=90°,即OP⊥PE. 小结:(1)证切线,连接圆心与该直线和圆的交点,只要证所作半径与该直线垂直即可.如本例证PE为切线,连接OP,只要证OP⊥PE即可. (2)直径所对的圆周角是直角,如本例AB为直径,则∠APB=90°. (3)直角三角形斜边上的中线等于斜边的一半.如本例∠BPC=90°,BE=CE,则PE= |


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:022
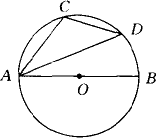
如下图所示,AB为⊙O的直径,AB=6,∠CAD=30°,则弦DC=________.
查看答案和解析>>
科目:初中数学 来源:新教材完全解读 九年级数学 下册(配北师大版新课标) 北师大版新课标 题型:044
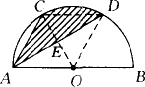
如下图所示,AB为半圆O的直径,C,D为半圆的三等分点,若AB=12,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2006年中考全真模拟试卷(二) 数学 题型:013
如下图所示,AB为半圆的直径,C为半圆上的一点,CD⊥AB于D,若CD=6,AD∶DB=3∶2,则AC·BC等于

A.![]()
B.![]()
C.![]()
D.90
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com