
 的边长为1,射线
的边长为1,射线 与射线
与射线 交于点
交于点 ,射线
,射线 与射线
与射线 交于点
交于点 ,
, .
.
 在线段
在线段 上时,试猜想线段
上时,试猜想线段 、
、 、
、 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想. ,
, ,当点
,当点 在线段
在线段 上运动时(不包括点
上运动时(不包括点 、
、 ),如图1,求
),如图1,求 关于
关于 的函数解析式,并指出
的函数解析式,并指出 的取值范围.
的取值范围. 在射线
在射线 上运动时(不含端点
上运动时(不含端点 ),点
),点 在射线
在射线 上运动.试判断以
上运动.试判断以 为圆心以
为圆心以 为半径的
为半径的 和以
和以 为圆心以
为圆心以 为半径的
为半径的 之间的位置关系.
之间的位置关系.
 在
在 延长线上时,设
延长线上时,设 与
与 交于点
交于点 ,如图2.问△
,如图2.问△ 与△
与△ 能否相似,若能相似,求出
能否相似,若能相似,求出 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.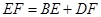 ,证明见解析 (2)
,证明见解析 (2) 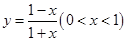 (3)当点
(3)当点 在线段
在线段 上时,
上时, 与
与 外切;当点
外切;当点 在
在 延长线上时,
延长线上时, 与
与 内切.(4)相似,所求
内切.(4)相似,所求 的长为
的长为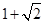
 . (1分)
. (1分)
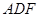 绕着点
绕着点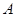 按顺时针方向旋转
按顺时针方向旋转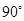 ,得△
,得△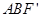 ,
,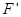 、
、 、
、 在一直线上.图1. (1分)
在一直线上.图1. (1分)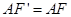 ,
,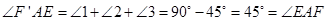 ,
,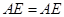 ,
,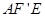 ≌△
≌△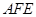
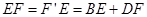 . (1分)
. (1分)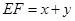
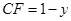 ,
,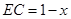 ,
,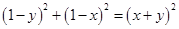 (1分)
(1分)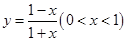 . (1+1分)
. (1+1分) 在点
在点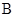 、
、 之间时,由(1)知
之间时,由(1)知 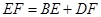 ,故此时
,故此时 与
与 外切;(1分)
外切;(1分) 在点
在点 时,
时,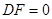 ,
, 不存在.
不存在. 在
在 延长线上时,
延长线上时,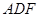 绕着点
绕着点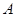 按顺时针方向旋转
按顺时针方向旋转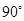 ,得△
,得△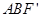 ,图2.
,图2.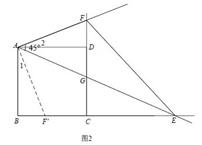
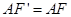 ,
,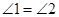 ,
,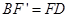 ,
, 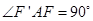 .
.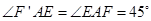 .
.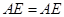 ,
,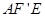 ≌△
≌△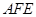 . (1分)
. (1分)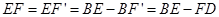 . (1分)
. (1分) 与
与 内切. (1分)
内切. (1分) 在线段
在线段 上时,
上时, 与
与 外切;当点
外切;当点 在
在 延长线上时,
延长线上时, 与
与 内切.
内切. 与△
与△ 能够相似,只要当
能够相似,只要当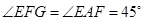 即可.
即可.
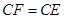 . (1分)
. (1分)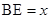 ,
, ,由(3)有
,由(3)有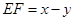
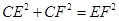 ,得
,得 .
.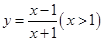 . (1分)
. (1分)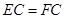 ,得
,得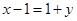 ,即
,即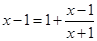 ,化简得
,化简得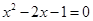 , (1分)
, (1分)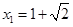 ,
,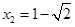 (不符题意,舍去) (1分)
(不符题意,舍去) (1分) 的长为
的长为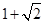 .
.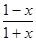 (0<x<1).
(0<x<1).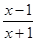 (x>1).又由 EC=FC,得x-1=1+y,即x-1=1+
(x>1).又由 EC=FC,得x-1=1+y,即x-1=1+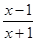 ,化简得x2-2x-1=0,解之即可求得BE的长.
,化简得x2-2x-1=0,解之即可求得BE的长.

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且 米,
米,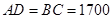 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道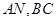 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于 处,
处, 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.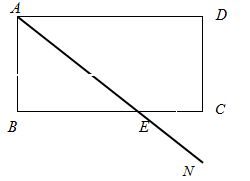
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
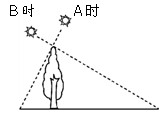
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com