
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{\sqrt{2}}{2}$ |
分析 根据等腰直角三角形的性质得出AC=CB=2,根据三角形的中线把三角形分成面积相等的两部分,利用面积计算即可.
解答 解:∵Rt△ABC中,∠ACB=90°,AC=CB,AB=2$\sqrt{2}$,
∴AC=CB=2,
∵CD是斜边AB的中线,
∴△DCB的面积=$\frac{1}{2}$△ABC的面积=$\frac{1}{2}×\frac{1}{2}×2×2$=1,
∴△DCB的面积=$\frac{1}{2}BC•$点D到BC的距离=$\frac{1}{2}×2$•点D到BC的距离=1,
∴点D到BC的距离=1,
故选A
点评 此题考查了等腰直角三角形的性质,关键是根据三角形的中线把三角形分成面积相等的两部分分析.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=$\sqrt{7}$,则∠CPA=( )
如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=$\sqrt{7}$,则∠CPA=( )| A. | 120° | B. | 135° | C. | 150° | D. | 145° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
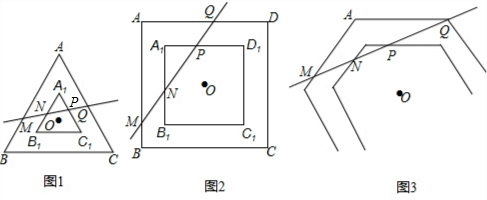
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从矩形ABCD中剪出一个圆心角为120°的扇形OBF,扇形OBF与CD相切,切点为E,用这个扇形围成一个圆锥.若矩形ABCD的面积为54,则围成的圆锥的高为4$\sqrt{2}$.
如图,从矩形ABCD中剪出一个圆心角为120°的扇形OBF,扇形OBF与CD相切,切点为E,用这个扇形围成一个圆锥.若矩形ABCD的面积为54,则围成的圆锥的高为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 4 | 2 | 2 | 1 |
| A. | 平均数是38.5 | B. | 众数是4 | C. | 中位数是40 | D. | 极差是3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com