
分析 (1)根据合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变,可得答案;
(2)合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变,可得答案;
(3)根据二次根式的乘除法,可得同类二次根式,再根据合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变,可得答案.
解答 解:原式=(3$\sqrt{2}$-5$\sqrt{2}$)+(4$\sqrt{3}$+$\frac{1}{2}$$\sqrt{3}$)
=-2$\sqrt{2}$+$\frac{9}{2}$$\sqrt{3}$;
(2)原式=(3$\sqrt{2a}$+4$\sqrt{2a}$)+(-5$\sqrt{5b}$-3$\sqrt{5b}$)
=7$\sqrt{2a}$-8$\sqrt{5b}$;
(3)原式=(3$\sqrt{2}$-$\frac{\sqrt{2}}{2}$+$\frac{2\sqrt{3}}{3}$)-($\frac{\sqrt{2}}{4}$-2$\sqrt{3}$)
=3$\sqrt{2}$-$\frac{\sqrt{2}}{3}$+$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{2}}{4}$+2$\sqrt{3}$
=(3$\sqrt{2}$-$\frac{\sqrt{2}}{3}$-$\frac{\sqrt{2}}{4}$)+($\frac{2\sqrt{3}}{3}$+2$\sqrt{3}$)
=$\frac{29\sqrt{2}}{12}$+$\frac{8\sqrt{3}}{3}$.
点评 本题考查了二次根式的加减,二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并;合并类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
圆的面积公式为s=πr2,其中变量是( )
A. s B. π C. r D. s和r
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省梅州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列运算正确的是( )
A. (3x3)2=9x6 B. 2x3•x2=2x6 C. x3+x2=x5 D. x6÷x3=x2
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省八年级下学期第一次月考数学试卷(解析版) 题型:填空题
从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 | 100 | 400 | 800 | 1 000 | 2 000 | 5 000 |
发芽种子粒数 | 85 | 318 | 652 | 793 | 1 604 | 4 005 |
发芽频率 | 0.850 | 0.795 | 0.815 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计,该玉米种子发芽的概率为 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:解答题
已知方程 的两个解是
的两个解是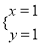 和
和
(1)求 、
、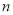 的值;
的值;
(2)用含有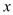 的代数式表示
的代数式表示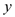 ;
;
(3)若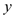 是不小于
是不小于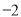 的负数,求
的负数,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com