
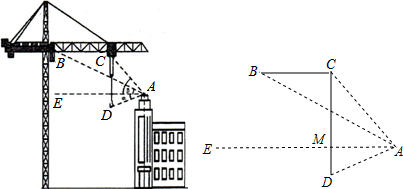
分析 过点A作AH⊥BC于点H,则△AHC,△AHB均为Rt△,设CH=xm,根据锐角三角函数的定义用x表示出AH的长,在Rt△ABH中,根据AH=BH•tan27°求出x的值,由四边形AHCM是矩形得出AM的长,在Rt△AMD中根据DM=AM•tan22°即可得出结论.
解答 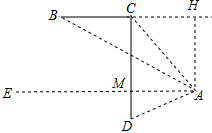 解:过点A作AH⊥BC于点H,
解:过点A作AH⊥BC于点H,
则△AHC,△AHB均为Rt△,设CH=xm,
∵HC∥AE,
∴∠HCA=∠CAE=50°,
∴AH=x•tan50°=1.19x.
∵HB∥AE,
∴∠HBA=∠BAE=27°,
∴在Rt△ABH中,AH=BH•tan27°,
则1.19x=(x+30)•tan27°,即1.19x=0.51(x+30),解得x=22.5.
∵四边形AHCM是矩形,
∴AM=22.5m.
在Rt△AMD中,DM=AM•tan22°=22.5×0.4=9.0m.
因此,吊钩需向右、向上分别移动22.5米、9.0米才能将材料送达A处.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | p=1,q=-12 | B. | p=-1,q=-12 | C. | p=7,q=12 | D. | p=7,q=-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
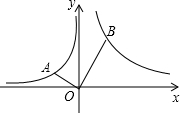 如图A,B两点分别在反比例函数y=-$\frac{1}{x}$(x<0)和y=$\frac{k}{x}$(k>0,x>0)的图象上,连接OA、OB,若OA⊥OB,OB=2OA,则k的值为( )
如图A,B两点分别在反比例函数y=-$\frac{1}{x}$(x<0)和y=$\frac{k}{x}$(k>0,x>0)的图象上,连接OA、OB,若OA⊥OB,OB=2OA,则k的值为( )| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com