
如图,⊙O与 的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知
的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知 ,⊙O的半径为12,弧DE的长度为
,⊙O的半径为12,弧DE的长度为 .
.

(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
(1)证明见解析;(2)60.
【解析】
试题分析:(1)要证明DE∥BC,可证明∠EDA=∠B,由弧DE的长度为4π,可以求得∠DOE的度数,再根据切线的性质可求得∠EDA的度数,即可证明结论.
(2)根据90°的圆周角对的弦是直径,可以求得EF,的长度,借用勾股定理求得AE与CF的长度,即可得到答案.
试题解析:(1)证明:连接OD、OE,

∵AD是⊙O的切线,
∴OD⊥AB,∴∠ODA=90°,
又∵弧DE的长度为4π,
∴4π= ,
,
∴n=60,
∴△ODE是等边三角形,
∴∠ODE=60°,∴∠EDA=30°,
∴∠B=∠EDA,
∴DE∥BC.
(2)连接FD,

∵DE∥BC,
∴∠DEF=∠C=90°,
∴FD是⊙0的直径,
由(1)得:∠EFD= ∠EOD=30°,FD=24,
∠EOD=30°,FD=24,
∴EF=12 ,
,
又∵∠EDA=30°,DE=12,
∴AE=4 ,
,
又∵AF=CE,∴AE=CF,
∴CA=AE+EF+CF=20 ,
,
又∵tan∠ABC=tan30°=
∴BC=60.
考点:1切线的性质;2.弧长的计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年山东省东营市九年级上学期期末模拟考试一数学试卷(解析版) 题型:选择题
如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=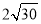 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )

A.6 B.8 C. 10 D.12
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在 中,
中, ,
, ,
, .点
.点 、
、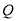 都是斜边
都是斜边 上的动点,点
上的动点,点 从
从 向
向 运动(不与点
运动(不与点 重合),点
重合),点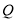 从
从 向
向 运动,
运动, .点
.点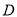 、
、 分别是点
分别是点 、
、 以
以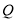 、
、 为对称中心的对称点,
为对称中心的对称点, 于
于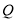 ,交
,交 于点
于点 .当点
.当点 到达顶点
到达顶点 时,
时, 、
、 同时停止运动.设
同时停止运动.设 的长为
的长为 ,
, 的面积为
的面积为 .
.

(1)求证: ∽
∽ ;
;
(2)求 关于
关于 的函数解析式;
的函数解析式;
(3)当 为何值时,
为何值时, 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
三角形的外心是( ).
A.各内角的平分线的交点
B.各边中线的交点
C.各边垂线的交点
D.各边垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期第二次双周测试数学试卷(解析版) 题型:填空题
在圆心角为120°的扇形AOB中,半径OA=6cm,则扇形AOB的面积是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期第二次双周测试数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1).则代数式1-a-b的值为( )
A.-3 B.-1 C.2 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(10分)在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在 轴的正半轴上,连结CE、AD、
轴的正半轴上,连结CE、AD、
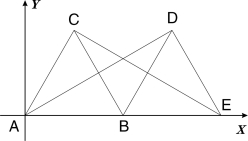
(1)求证:AD=CE;
(2)求AD的长;
(3)求过C、E两点的直线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com