练习册

  • 练习册
  • 试题
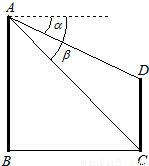
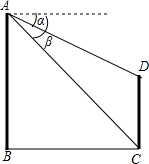    精英家教网 > 初中数学 > 题目详情
    如图，已知两座大楼的水平距离BC为100米，站在大楼AB楼顶A测得大楼CD楼顶D的俯角α为35°，楼底C的俯角β为43°，求两大楼的高度．（sin35°=0.574，cos35°=0.819，tan35°=0.700，sin43°=0.682，cos43°=0.731，tan43°=0.933）

    【答案】分析：设AE=x，根据AE和α即可求得DE的长度，根据AE和β即可求得CE的长度，根据CD=CE-DE即可求得x的值，即可解题．
    解答：解：设AE=x，
    在Rt△ADE中，DE=AE•tanα
    在Rt△ACE中，CE=AE•tanβ
    ∵CD=CE-DE=100米，
    即x（tanβ-tanα）=100，
    解得x=米=429.18米．
    点评：本题考查了三角形中三角函数的应用，本题中分别求CE、DE的长是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，已知两座大楼的水平距离BC为100米，站在大楼AB楼顶A测得大楼CD楼顶D的俯角α为35°，楼底C的俯角β为43°，求两大楼的高度．（sin35°=0.574，cos35°=0.819，tan35°=0.700，sin43°=0.682，cos43°=0.731，tan43°=0.933）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

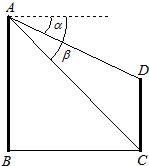    精英家教网如图，已知两座大楼的水平距离BC为100米，站在大楼AB楼顶A测得大楼CD楼顶D的俯角α为35°，楼底C的俯角β为43°，求两大楼的高度．（sin35°=0.574，cos35°=0.819，tan35°=0.700，sin43°=0.682，cos43°=0.731，tan43°=0.933）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•安庆二模）如图是某小区的两座高楼，小明乘坐观光电梯在C处测得另一大楼顶部A的仰角为37°，电梯下降10m到D处时，又测得其底部B的俯角为48°．已知两座楼都为30层，每层高约2.8m，请帮小明求出两座高楼间的距离（参考数据：sin37°≈
    3
    5
    ，tan37°≈
    3
    4
    ，sin48°≈
    7
    10
    ，tan48°≈
    11
    10
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知两座大楼的水平距离BC为100米，站在大楼AB楼顶A测得大楼CD楼顶D的俯角α为35°，楼底C的俯角β为43°，求两大楼的高度．（sin35°=0.574，cos35°=0.819，tan35°=0.700，sin43°=0.682，cos43°=0.731，tan43°=0.933）

    查看答案和解析>>

    同步练习册答案