
【题目】如图,在下列5×5的网格中,横、纵坐标均为整点的数叫做格点,例如A(0,1)、B(2,1)、C(3,3)都是格点,仅用无刻度的直尺在网格中做如下操作:
(1)直接写出点A关于点B旋转180°后对应点M的坐标 ;
(2)画出线段BE,使BE⊥AC,其中E是格点,并写出点E的坐标 ;
(3)找格点F,使∠EAF=∠CAB,画出△EAF,并写出点F的坐标 ;
(4)找格点D(D与B不重合),使S△ABC=S△ACD,直接写出格点D的坐标 .

【答案】(1)(4,1);(2)图详见解析,点E的坐标(0,4);(3)图详见解析,点F的坐标(2,4);(4)(1,3)或(5,3).
【解析】
(1)根据图形直接得出;
(2)利用2×3的长方形的对角线,即可得到线段BE⊥AC;
(3)利用直角边为2和3的直角三角形,即可得到点F;
(4)利用三角形面积相等时,如果高相等则底边相等,即可得到点D.
解:(1)如图1所示,点A关于点B旋转180°后对应点M的坐标为:(4,1);
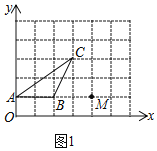
故答案为:(4,1);
(2)如图2所示,线段BE即为所求;

则点E的坐标为(0,4);
故答案为:(0,4);
(3)如图3所示,点F即为所求,其坐标为(2,4);
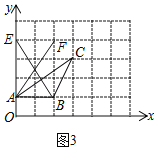
故答案为:(2,4);
(4)如图4所示,点D即为所求,其坐标为(1,3)或(5,3);
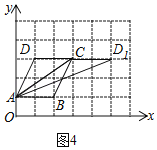
故答案为:(1,3)或(5,3).


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小组做用频率估计概率“的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
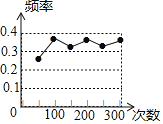
A. 抛一枚硬币,出现正面朝上
B. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 掷一枚均匀的正六面体骰子,出现3点朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为()cm2.
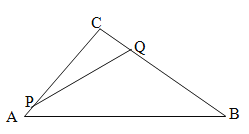
A. 19 B. 16 C. 15 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为![]() 上一点,且
上一点,且![]() ,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③
,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③![]() ;④∠ACM+∠ANM=∠MOB;⑤AE=
;④∠ACM+∠ANM=∠MOB;⑤AE=![]() MF.
MF.
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
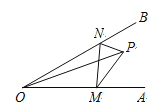
【题目】如图,∠AOB![]() 30°,点P是∠AOB内的一定点,且OP
30°,点P是∠AOB内的一定点,且OP![]() 6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
6,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com