Question

9．如图A是棱长为1的小正方体，图B、图C由这样的小正方体摆放而成．按照这样的方法继续摆放，自上而下分别叫做第1层、第2层、…、第n层，第n层的小正方体的个数记做t，请解答下列问题．

（1）按要求填表：

层数	1	2	3	4	…	n
t	1	3	6	10	…	$\frac{n（n+1）}{2}$

（2）求当n=10时，该组合体的表面积为多少？

Answer 1

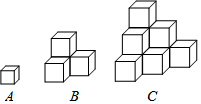
分析 （1）第1个图有1层，共1个小正方体，第2个图有2层，第2层正方体的个数为1+2…根据相应规律可得第n层正方体的个数为1+2+3+…+n=$\frac{n（n+1）}{2}$；
（2）根据上、下、左、右、前、后看到小正方形的面的个数各为55，求出总面数再乘每一个小正方形的面积即可．

解答 解：（1）填表如下：

层数	1	2	3	4	…	n
t	1	3	6	10	…	$\frac{n（n+1）}{2}$

（2）1×1×（$\frac{10×（10+1）}{2}$×6）
=1×330
=330．
答：该组合体的表面积为330．
故答案为：6，10，$\frac{n（n+1）}{2}$．

点评 此题考查图形规律性的变化；得到第n层正方体的个数的规律是解决本题的关键．