
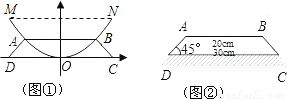
 AB=10cm,在直角三角形BFC中,FC=
AB=10cm,在直角三角形BFC中,FC= (CD-AB)=5cm,∠BCF=45°,即可求出BF的长,也就得出了B点的坐标,A、B关于y轴对称,也就能求出A点的坐标;
(CD-AB)=5cm,∠BCF=45°,即可求出BF的长,也就得出了B点的坐标,A、B关于y轴对称,也就能求出A点的坐标;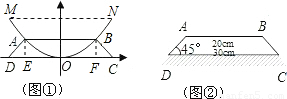 解:(1)作AE⊥DC,BF⊥DC,垂足分别为E,F,
解:(1)作AE⊥DC,BF⊥DC,垂足分别为E,F, (30-20)=5
(30-20)=5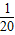 ,
,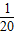 x2,
x2,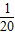 x2得y=
x2得y=
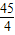 cm;
cm;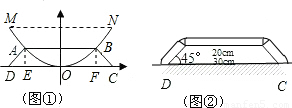
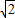 ×2+20+30+
×2+20+30+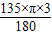 ×2+
×2+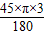 ×2=10
×2=10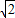 +50+6π.
+50+6π.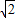 +50+6π)cm.
+50+6π)cm.

 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
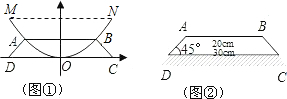 m的保护膜,如图②,请在图中补充完整镀膜部分的示意图,并求出镀膜的外围周长.
m的保护膜,如图②,请在图中补充完整镀膜部分的示意图,并求出镀膜的外围周长.查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(37):2.8 二次函数的应用(解析版) 题型:解答题
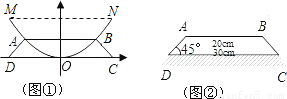
查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(33):23.5 二次函数的应用(解析版) 题型:解答题
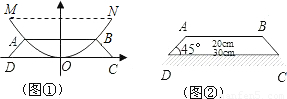
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
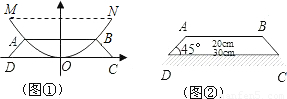
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com