Question

6．在直角梯形ABCD中，AD∥BC，∠B=90°，AB=11．
（1）若AD=2，BC=5，点E在AB上，当△ADE与△BCE相似时，求AE的长；
（2）若AD=a，BC=b，点Q在AB上，则当a、b满足什么条件时，有且只有一个点Q，使得∠DQC=90°．

Answer 1

分析 （1）如图1，当△ADE与△BCE相似时，因为△ADE与△BCE都是直角三角形，所以要分两种情况讨论：①当△ADE∽△BEC时，②当△ADE∽△BCE时，列比例式代入计算即可；
（2）证明△DAQ∽△QBC，列比例式，得方程，因为有且只有一个点Q，所以方程有两个相等的实数解，△=0，所以得ab=$\frac{121}{4}$．

解答 解：（1）设AE=x，则BE=11-x，如图1，
①当△ADE∽△BEC时，
得$\frac{AD}{BE}=\frac{AE}{BC}$，
∵AD=2，BC=5，
∴$\frac{2}{11-x}=\frac{x}{5}$，
∴x=1或x=10，
∴AE=1或10，
②当△ADE∽△BCE时，
得$\frac{AD}{BC}=\frac{AE}{BE}$，
∴$\frac{2}{5}=\frac{x}{11-x}$，
∴x=$\frac{22}{7}$，
综上所述，当△ADE与△BCE相似时，求AE的长为1或10或$\frac{22}{7}$；
（2）如图2，∴∠DQC=90°，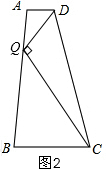
∴∠AQD+∠CQB=90°，
∵∠A=90°，
∴∠AQD+∠ADQ=90°，
∴∠ADQ=∠CQB，
∵∠A=∠B=90°，
∴△DAQ∽△QBC，
∴$\frac{AD}{BQ}=\frac{AQ}{BC}$，
∵AD=a，BC=b，
∴$\frac{a}{11-x}=\frac{x}{b}$，
x（11-x）=ab，
-x²+11x-ab=0，
x²-11x+ab=0，
△=（-11）²-4ab=0，
ab=$\frac{121}{4}$，
∴当a、b满足ab=$\frac{121}{4}$时，有且只有一个点Q，使得∠DQC=90°．

点评 本题考查了直角梯形，明确直角梯形的定义：有一个角是直角的梯形叫做直角梯形；当两个直角三角形相似时，要分两种情况进行讨论；在第（2）的求解中，与方程的解的情况相结合：方程有一个解时，△=0，以此作依据列式计算．