
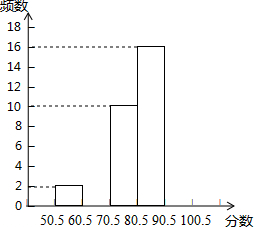
 某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)
某校对600名学生进行了一次“心理健康”知识测试,从中抽取了部分学生成绩(得分取正整数,满分为100分)作为样本,绘制了下面尚未完成的表格和频数分布直方图(住:无50.5以下成绩)| 分组 | 频数 | 频率 |
| 50.5~60.5 | 2 | 0.04 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | C |
| A~90.5 | B | 0.32 |
| 90.5~100.5 | 14 | 0.28 |
| 合计 |
分析 (1)利用组距为10cm可得到A的值,用第1组的频数除以它的频率得到样本容量,再用第4组的频率乘以样本容量可得B的值,然后用第3组的频数除以样本容量可得C的值;
(2)频数分布表得到第2组的频数为8,第5组的频数为14,则可补全频数分布直方图;
(3)用600乘以第5组的频率可估计该校成绩优秀人数.
解答 解:(1)A=80.5,
2÷0.04=50,
B=50×0.32=16,
C=10÷50=0.2;
故答案为80.5,16,0.2;
(2)如图,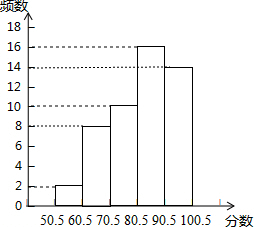
(3)600×0.28=168,
所以估计该校成绩优秀的有168人.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了用样本估计总体.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com