
分析 分子为1,分母为相邻2个自然数的分数应等于分子为1,分母分别为这两个自然数的分数的差,依此规律得到所要计算的式子的每个分数等于分子为1,分母分别为原分数中2个因数的分数的差的一半,进而化解计算即可.
解答 解:$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$,
$\frac{1}{2014×2015}$=$\frac{1}{2014}$-$\frac{1}{2015}$,
$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故答案为:$\frac{1}{4}$-$\frac{1}{5}$,$\frac{1}{2014}$-$\frac{1}{2015}$,$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$=$\frac{1}{2}$×($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+$\frac{1}{6}$-$\frac{1}{8}$+…+$\frac{1}{2014}$-$\frac{1}{2016}$)=$\frac{1}{2}$×($\frac{1}{2}$-$\frac{1}{2016}$)=$\frac{1007}{4032}$.
点评 此题考查数的变化规律的应用;得到分子为1,分母为2个等差的数的积的分数的化简规律是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,一次函数y=-x+2的图象分别交x、y轴于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0)且把△AOB的面积分成两部分.
如图,在平面直角坐标系中,一次函数y=-x+2的图象分别交x、y轴于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0)且把△AOB的面积分成两部分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
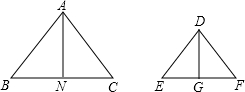 已知:在△ABC与△DEF中,AN⊥BC于N,DG⊥EF于G,$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$,求证:△ABC∽△DEF.
已知:在△ABC与△DEF中,AN⊥BC于N,DG⊥EF于G,$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$,求证:△ABC∽△DEF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线CE垂直于弦AD于点E,连OD交AC于点F.
如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线CE垂直于弦AD于点E,连OD交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 练习罚球次数 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 罚中次数 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 罚中频率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com