Question

15．如图，直线m：y=$\frac{b}{4}$x+b（b＞0）与x轴交于A点，与y轴交于C点，过C点的另一直线n交x轴正半轴于B点，且满足OA=2OB
①若∠ACB=90°，求直线n的解斩式；
②若∠ACB=45°，求b的值；
③若直线m上存在一点M，过M作MN∥x轴交直线n于点N点，直线m上存在另一点P．使得以M、O、N、P为顶点的四边形是矩形，求b的值（请直接写答案）．

Answer 1

分析 根据直线m的解析式求出点C、A的坐标，再根据OA、OB的关系可找出点B的坐标，利用两点间的距离公式求出AB、AC、BC的距离，由点B、C的坐标利用待定系数法即可求出直线n的解析式．
①在Rt△ACB中，利用勾股定理即可得出关于b的一元二次方程，解方程即可求出b值，再将b的值代入直线n的解析式中即可；
②过点B作BD⊥直线m于点D，在Rt△BCD中求出BD的长度，根据面积法即可得出关于b的一元四次方程，解方程即可得出b²值，结合①结论确定b²值，开方即可得出结论；
③过点O作OM⊥直线l于点M，过点M作MN∥x轴交直线n于点N，连接ON，过点N作NP⊥直线m于点P，根据矩形的性质即可得出∠MON=90°，再通过角的计算即可证出△OMN∽△OCA，结合勾股定理以及相似三角形的性质即可得出关于x、b的二元多次方程组，根据方程组中两方程的特点即可得出关于b的分式方程，解方程即可得出结论．

解答 解：令y=$\frac{b}{4}$x+b中x=0，则y=b，
∴C（0，b）；
令y=$\frac{b}{4}$x+b中y=0，则x=-4，
∴A（-4，0）．
∵OA=2OB，且点B在x轴正半轴上，
∴B（2，0）．
∴AB=2-（-4）=6，AC=$\sqrt{{b}^{2}+（-4）^{2}}$，BC=$\sqrt{{b}^{2}+{2}^{2}}$．
设直线n的解析式为y=kx+b（k≠0），
将点B（2，0）代入y=kx+b中，
得：0=2k+b，解得：k=-$\frac{b}{2}$，
∴直线n的解析式为y=-$\frac{b}{2}$x+b．
①在△ACB中，∠ACB=90°，
∴AB²=AC²+BC²，即6²=b²+（-4）²+b²+2²，
解得：b=2$\sqrt{2}$或b=-2$\sqrt{2}$（舍去），
∴直线n的解析式为y=-$\sqrt{2}$x+2$\sqrt{2}$．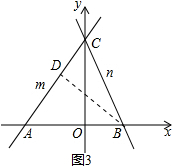
②过点B作BD⊥直线m于点D，如图3所示．
在△BCD中，∠BDC=90°，∠BCD=45°，
∴BD=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$$\sqrt{{b}^{2}+{2}^{2}}$．
∴S_△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$AC•BD，即6b=$\sqrt{{b}^{2}+（-4）^{2}}$•$\frac{\sqrt{2}}{2}$$\sqrt{{b}^{2}+{2}^{2}}$，
解得：b²=26+6$\sqrt{17}$或b²=26-6$\sqrt{17}$，
∵∠BCD=45°，
∴b＞2$\sqrt{2}$，
∴b²=26+6$\sqrt{17}$，
∴b=$\sqrt{17}$+3或b=-$\sqrt{17}$-3（舍去）．
故b的值为$\sqrt{17}$+3．
③过点O作OM⊥直线l于点M，过点M作MN∥x轴交直线n于点N，连接ON，过点N作NP⊥直线m于点P，如图所示．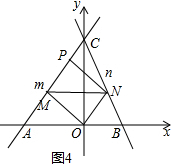
∵四边形MONP为矩形，
∴∠MON=90°．
设点M（x，$\frac{b}{4}$x+b），则N（-$\frac{x}{2}$，$\frac{b}{4}$x+b），
∴MN=-$\frac{x}{2}$-x=-$\frac{3}{2}$x，OM=$\sqrt{{x}^{2}+（\frac{b}{4}x+b）^{2}}$，ON=$\sqrt{（-\frac{x}{2}）^{2}+（\frac{b}{4}x+b）^{2}}$．
在Rt△MON中，∠MON=90°，
∴MN²=OM²+ON²，即x²=2$（\frac{b}{4}x+b）^{2}$（i）；
∵MN∥x轴，
∴∠CMN=∠A，
OM⊥直线m于点M，
∴∠OMC=90°，
∵∠A+∠OCA=90°，∠OMN+∠CMN=90°，
∴∠OMN=∠OCA．
∵∠MON=∠COA=90°，
∴△OMN∽△OCA，
∴$\frac{ON}{OA}=\frac{OM}{OC}$，即（16-b²）$（\frac{b}{4}x+b）^{2}$=$\frac{{b}^{2}}{4}{x}^{2}$-16x²（ii）．
联立（i）（ii）成方程组，$\left\{\begin{array}{l}{{x}^{2}=2（\frac{b}{4}x+b）^{2}}\\{（16-{b}^{2}）（\frac{b}{4}x+b）^{2}=\frac{{b}^{2}}{4}{x}^{2}-16{x}^{2}}\end{array}\right.$，
∴$\frac{\frac{{b}^{2}}{4}-16}{16-{b}^{2}}=\frac{1}{2}$，
解得：b=4$\sqrt{2}$或b=-4$\sqrt{2}$（舍去）．
经检验b=4$\sqrt{2}$是方程$\frac{\frac{{b}^{2}}{4}-16}{16-{b}^{2}}=\frac{1}{2}$的解．
故：当直线m上存在一点M，过M作MN∥x轴交直线n于点N点，直线m上存在另一点P，使得以M、O、N、P为顶点的四边形是矩形时，b的值为4$\sqrt{2}$．

点评 本题考查了待定系数法求函数解析式、三角形的面积以及矩形的性质，解题的关键是：①利用勾股定理找出关于b的一元二次方程；②根据三角形的面积找出关于b的一元四次方程；③找出关于b的分式方程．本题属于中档题，难度不大，解决该题型题目时，利用勾股定理（或相似三角形的性质）找出方程是关键．