
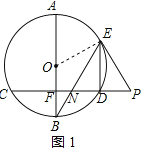
【题目】在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P在CD的延长线上,PN=PE.
(1)求证:PE是⊙O的切线;
(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.
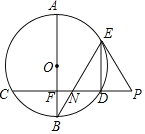
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OE,由等腰三角形的性质得出∠PEN=∠PNE=∠BNF,∠OEB=∠OBE.证出∠OEB+∠PEN=90°,即PE⊥OE,即可得出结论;
(2)连接CE,证出CE为⊙O的直径.由垂径定理得出CF=DF,得出DE=2OF=6.求出OC=OB=5,CE=10,由勾股定理得出CD=8.设PD=x,则PC=x+8.在Rt△PDE和Rt△PCE中,由勾股定理得出方程,解方程求出PD=![]() ,由勾股定理即可得出答案.
,由勾股定理即可得出答案.
(1)证明:连接OE,如图1所示:
∵PN=PE,
∴∠PEN=∠PNE=∠BNF,
∵OE=OB,
∴∠OEB=∠OBE.
∵AB⊥CD,
∴∠OBE+∠BNF=90°,
∴∠OEB+∠PEN=90°,
即∠OEP=90°,
∴PE⊥OE,
∴PE是⊙O的切线.
(2)解:连接CE,如图2所示:
∵DE∥AB,AB⊥CD,
∴∠EDC=90°
∴CE为⊙O的直径.
∵AB⊥CD,
∴CF=DF,∴DE=2OF=6.
∵OF=3,BF=2,∴OC=OB=5,CE=10,
∴CD=![]() =
=![]() =8,
=8,
由(1)知PE⊥CE.设PD=x,则PC=x+8.
在Rt△PDE和Rt△PCE中,由勾股定理,得:PD2+DE2=PE2=PC2-CE2,
即x2+62=(x+8)2-102,
解得:x=![]() ,
,
∴PD=![]() .
.
∴PE=![]() =
=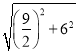 =
=![]() ,
,
∴PN=PE=![]() .
.



科目:初中数学 来源: 题型:
【题目】某公司从2016年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年度 | 投入技改资金x/万元 | 产品成本y/(万元/件) |
2016 | 2 | 18 |
2017 | 3 | 12 |
2018 | 4 | 9 |
2019 | 4.5 | 8 |
(1)根据表格中数据,求y关于x的函数解析式。
(2)在图中的网格中建立适当的平面直角坐标系,画出该函数的大致图像。
(3)如果打算在2020年让产品成本不高于7万元,则投入技改资金至少为 万元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() .
.
(1)当![]() 时,若点
时,若点![]() 在该二次函数的图象上,求该二次函数的表达式;
在该二次函数的图象上,求该二次函数的表达式;
(2)已知点![]() ,
,![]() 在该二次函数的图象上,求
在该二次函数的图象上,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,若该二次函数的图象与直线
时,若该二次函数的图象与直线![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与直线x=2相交于点A,将抛物线y=x2沿线段OA从点O运动到点A,使其顶点始终在线段OA上,抛物线与直线x=2相交于点P,则点P移动的路径长为( )

A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有6张看上去无差别的卡片,上面分别写着1、2、3、4、5、6
(1)一次性随机抽取2张卡片,用列表或画树状图的方法求出“两张卡片上的数都是偶数”的概率
(2)随机摸取1张后,放回并混在一起,再随机抽取1张,直接写出“第二次取出的数字小于第一次取出的数字”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(小球除颜色外其余都相同),其中黄球2个,蓝球1个.若从中随机摸出一个球,摸到蓝球的概率是![]() .
.
(1)求口袋里红球的个数;
(2)第一次随机摸出一个球(不放回),第二次再随机摸出一个球,请用列表或画树状图的方法,求两次摸到的球恰是一黄一蓝的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=ax2+bx﹣3的对称轴为直线x=1,且该抛物线经过点(3,0).
(1)求该抛物线对应的函数表达式.
(2)当﹣2≤x≤2时,则函数值y的取值范围为 .
(3)若方程ax2+bx﹣3=n有实数根,则n的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在八月十五“中秋节”来临前夕,购进一种品牌的月饼,每盒进价40元,根据以往的销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
![]() 写出每天的销售量
写出每天的销售量![]() 盒
盒![]() 与每盒月饼上涨
与每盒月饼上涨![]() 元
元![]() 之间的函数关系式.
之间的函数关系式.
![]() 当每盒售价定为多少元时,当天的销售利润
当每盒售价定为多少元时,当天的销售利润![]() 元
元![]() 最大?最大利润是多少?
最大?最大利润是多少?
![]() 为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的
为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的![]() ,那么超市每天获得最大利润是多少?
,那么超市每天获得最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com