
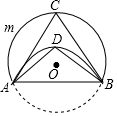
 如图,将⊙O沿弦AB折叠,点C在$\widehat{AmB}$上,点D在$\widehat{AB}$上,若∠ACB=70°,则∠ADB=110°.
如图,将⊙O沿弦AB折叠,点C在$\widehat{AmB}$上,点D在$\widehat{AB}$上,若∠ACB=70°,则∠ADB=110°.  名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
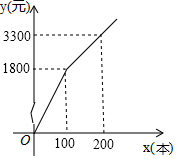 某书店为了迎接2017年4月23日的“世界读书日”,计划购进A、B两类图书进行销售,若购进A、B两类图书共1000本,其中购进A类图书的单价为16元/本,购进B类图书所需费用y(元)与购买数量x(本)之间存在如图所示的函数关系.
某书店为了迎接2017年4月23日的“世界读书日”,计划购进A、B两类图书进行销售,若购进A、B两类图书共1000本,其中购进A类图书的单价为16元/本,购进B类图书所需费用y(元)与购买数量x(本)之间存在如图所示的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
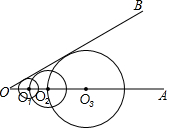 如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是29.
如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是29.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
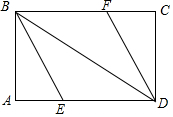 如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
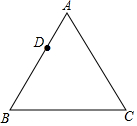 如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com